AMC10/12/AIME的解题技巧

夏令营期间，我们也有幸请到AIME委员会主席、AMC和USAMO委员会成员Dr. Kane，为备战AMC10/12和AIME的学员们做线上讲座。讲座上，Dr. Kane为大家整理了10种独家解题技巧。

为什么要学习这些解题技巧呢？

Dr. Kane解释，如果你对一道题目感到陌生，不确定该用什么解题思路去回答时，该怎么办？这时你可以利用已知几个解题方法去观察问题：找出问题的规律、先解出简单情况下的答案，尝试找出和课堂知识的连接点，可以有效地帮助你完成解题过程。

有哪些解题技巧？

01寻找规律

将方程的结果列成一个数字序列。观察数字之间是否有相等的差异，或者是否有一些数字重复出现。

这可能会揭示出一些数列或等差数列的模式。有时候规律可能很明显，有时候可能需要多次尝试和思考。不断练习寻找规律的技巧，可以帮助你更好地解决各种数学问题。

例子：

02尝试解简单的情况

尝试将方程中的变量取一些简单的值，例如0、1、-1，看看是否能够发现某种规律或性质。这些简单值可能会揭示出方程的一些特征。通过尝试解决问题的简单情况，你可以更深入地理解问题，找到问题的规律和解决方法。

这种方法还可以帮助你建立起解决问题的直觉，从而更有效地应对更复杂的情况。

例子：How many positive integers are divisors of either 20^20 or 50^20?

03画图

将方程的结果绘制成图表，可能是折线图、柱状图等。这可以帮助你直观地看到数据的趋势和模式。通过画图，你可以更直观地理解问题，从而更容易找到解决方法。画图也有助于将抽象的数学概念转化为具体的可视化表示，使问题更加实际和具体。

例子：How many real numbers x satisfy 100 sin(πx) = x^2?

04把它拆分成更简单的问题

如果方程中有一些复杂的部分，尝试化简它们，例如提取公因式、合并同类项。这可能会使方程变得更加可控和易于处理。通过将复杂的问题拆分成更小、更简单的子问题，你可以更有针对性地解决每个子问题，最终得到整体问题的解答。这个过程有助于提高问题的可解性和你对问题的理解。

例子：Let a, b, c be positive integers such that abc+bc+c = 2014. Find the minimum possible value of a + b + c.

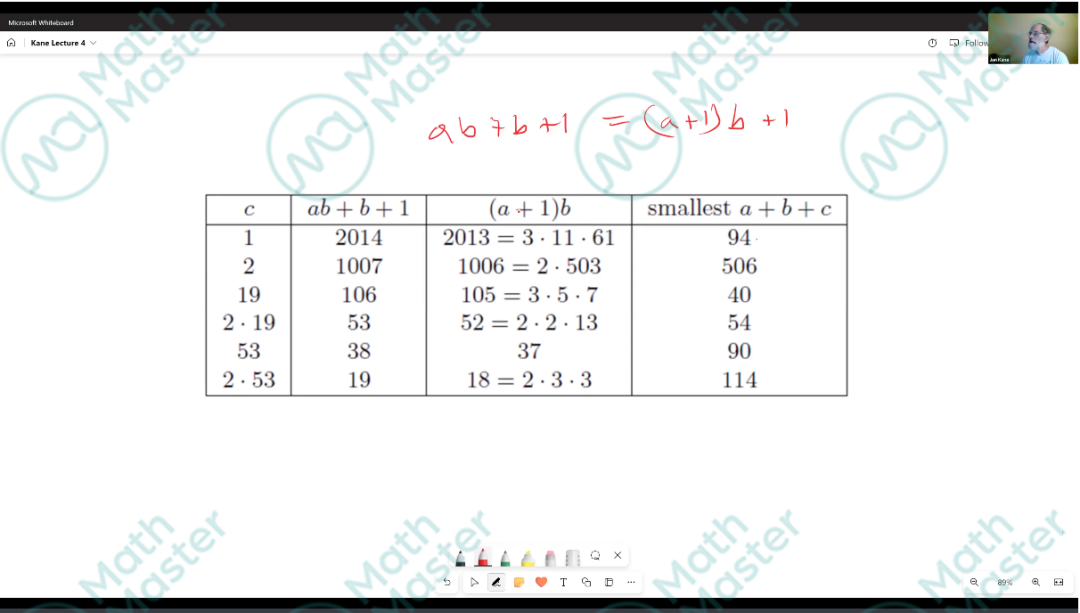
05逆向思考

逆向思考意味着从问题的解决方向反向推导，从已知条件或最终目标出发，逐步找出连接它们的路径。逆向思考需要耐心和逻辑性，但它可以帮助你从一个不同的角度来解决问题，找到可能的解决方案。在实践中，结合正向和逆向思考，可以更全面地理解问题，找到更好的解决方案。

例子：Find the value of the expression S = 1!·3 - 21·4+3!·5 - 4!·6 + ... - 2006!·2008 + 2007!

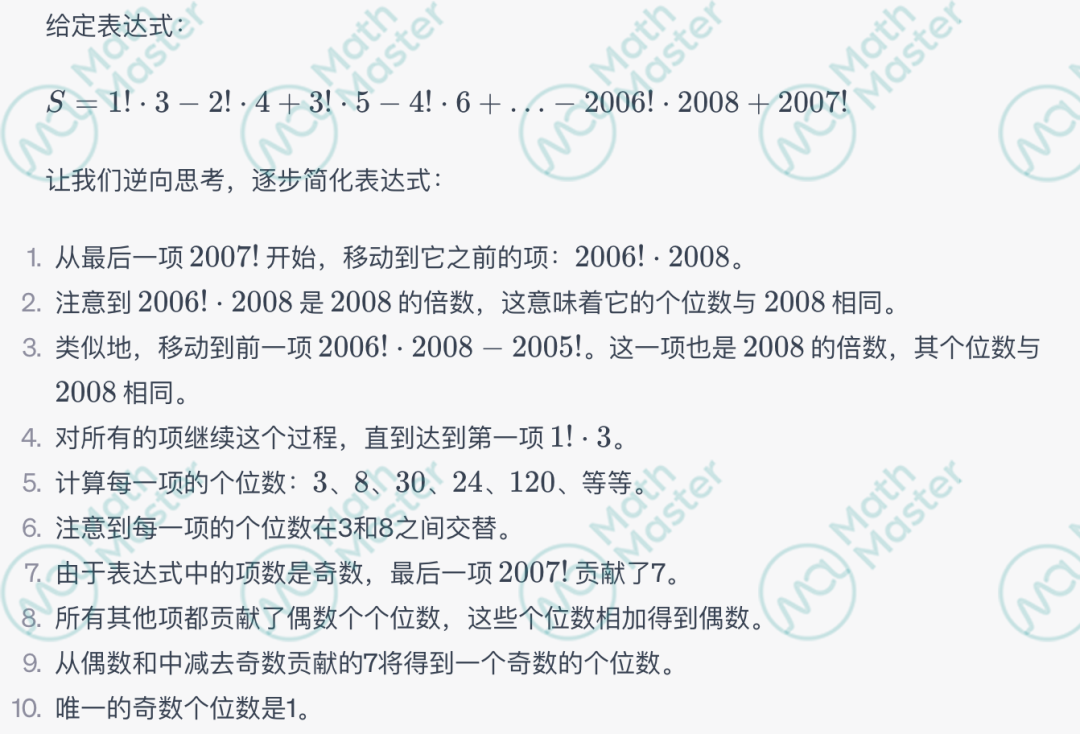
06将你所知道的一切写下来

将你所知道的一切写下来。当你面对一道题毫无头绪时，可以将自己所知道的写下来。将你所知道的一切写下来是非常重要的，可以帮助你更清晰地理解问题，整理思路，以及避免遗漏关键信息。这个步骤可以帮助您整理思路、澄清问题，并为后续的推导和解决方案提供指导。

例子：在梯形ABCD中，AD||BC，AB = AD + BC，并且E是CD的中点。证明角<BAD和角<ABC的角平分线都经过点E。

07考虑极端情况

将变量取极限值，例如趋近于正无穷大或负无穷大，看看方程的行为如何。它可以用于帮助你理解问题的特性，发现规律，或者证明某个结论。考虑极端情况可以帮助你从不同的角度看待问题，发现问题的规律和特点，进而更好地解决问题、证明结论或得出答案。在实际解题过程中，多练习考虑极端情况的方法，你会逐渐培养出更深入的问题分析和推理能力。

例子：Prove that there are no positive integers a and b such that both 2a^2 + b^2 and a^2 + 26^2 are perfect squares.

08寻找矛盾点

使用问题中的基本性质和条件，尝试从中推导出与问题要求相悖的结论。寻找矛盾点是一种有用的策略，可以帮助您识别不一致或不合理的情况，从而揭示可能的错误或问题。当你把错误的答案逐个剔除，得到正确答案的概率增加。

例子：Show that for any three real numbers x, y, and z, the following inequalities cannot be all true. |x|<|y-z|；|y|<|z-x|；|z|<|x-y|

09计算

对于向量问题，可以使用向量来表示方向和位移。利用向量的性质进行计算，比如向量的相加、相减、数量积等。在进行计算的同时，要时刻保持警惕，避免计算错误。在每一步都要检查计算是否正确，避免累积计算错误。

例子：Two frogs jump around on the lattice points (points with integer coordinates) on the coordinate plane. One frog starts at the point (3,-7), and the other frog starts at the point (-6; 1). Each minute both frogs jump from wherever they are to another lattice point one unit from where they are. Show that the two frogs cannot both land on the point (9, 2) at the same time.

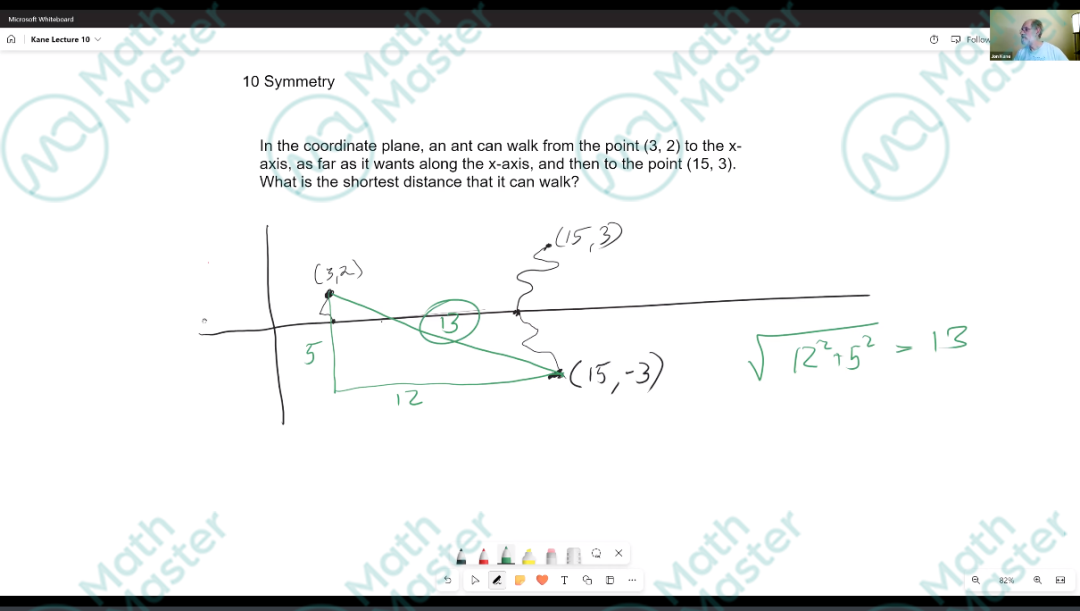
10利用对称性

如果方程具有对称性，例如关于某个轴对称或旋转对称，尝试利用这些特性简化方程。利用对称性可以帮助简化问题、发现规律以及得出结论。在解题过程中，多考虑问题中存在的对称性质，并灵活运用它们来解决问题。

例子：In the coordinate plane, an ant can walk from the point (3, 2) to the x-axis, as far as it wants along the x-axis, and then to the point (15, 3). What is the shortest distance that it can walk?

在解题的道路上，掌握解题技巧是迈向成功的关键一步。正如Dr. Kane在讲座中所强调的，解题技巧不仅是解决复杂问题的工具，更是培养逻辑思维、提升问题解决能力的途径。

当我们面对陌生的问题时，常常感到无从下手，迷失在问题的迷雾中。然而，正是在这样的时刻，学会运用不同的解题方法，像是寻找问题规律、逐步解决简单情况、与课堂知识建立联系等，才能为我们点亮前行的道路。