AMC8有哪些解题技巧？

在2023年夏令营，我们有幸邀请到AIME委员会主席、AMC和USAMO委员会成员Dr. Kane，为备战AMC8的学员们做线上讲座。在讲座上，Dr. Kane用他丰富的教学经验为大家总结整理了一些独家解题技巧，令不少学生茅塞顿开。

那么这些解题技巧该在什么时候使用呢？它们的应用场景是怎么样的？

赶紧查收讲座干货第三弹，看Dr. Kane如何手把手教你使用答题秘笈！

有哪些解题技巧？

01寻找规律

应用场景：遇到的问题中包含一些大数字或者需要自己通过计算得到一个大的数字。这个时候就可以尝试寻找一种规律，例题如下：

除此之外，我们还可以尝试另外一种解法。

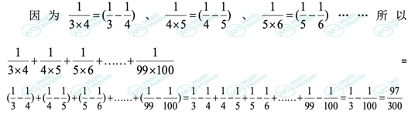
02尝试解简单的情况

应用场景：当你遇到一个很复杂的问题时，也许你可以尝试通过观察一个简单的类似的题目来为你解决复杂题目提供帮助。

例子：现有一个面积为1 X 10的方块需要贴瓷砖，可选的瓷砖有面积为1X1的红砖和面积为1X2的绿砖，请问可以选择多少种方式来张贴瓷砖？

很明显，我们可以用 1X1 的红砖填满方块或者用五个1X2的绿砖填满，也可以使用一些红砖和绿砖搭配的方案。但我们依旧很难计算出到底有多少种搭配的方案。

那么，我们为什么不先解决一个更简单的问题呢？

首先，在红砖和绿砖的条件不变的前提下，请思考以下几个问题。

一个1X1的方块有几种贴法？答案是一种——用一个红砖。

一个1X2的方砖有几种贴法？答案是两种——用两个红砖或一个绿砖。

一个1X3的方砖有几种贴法？答案是三种——用三个红砖、先贴一个绿砖再贴一个红砖或者先贴一个红砖再贴一个绿砖。

一个1X4的方砖有几种贴法？答案是五种——用四个红砖、两个绿砖、一个绿砖两个红砖、一个红砖一个绿砖一个红砖、两个红砖一个绿砖。

以此类推，可以得到1X10的情况。

03画图

应用场景：当你遇到的问题条件十分适合绘制图形且绘制图形能帮助你了解哪些定理适用于解决该问题时，你就可以选择用画图的方式。

例子：两根垂直的杆子相距6米。一个是10米高，另一个是8米高。两根电线从每根电线杆的顶部延伸到另一根电线杆底部。电线交叉的高度是多少？

接下来，可以把我们要求的高度设为ｈ（即两根电线交叉点向地面作垂直所得的线段为ｈ），ｈ在地面形成的点分别连接两条电线杆，连接0米高杆子的线段设为ｘ，另一条线段则为6-x。

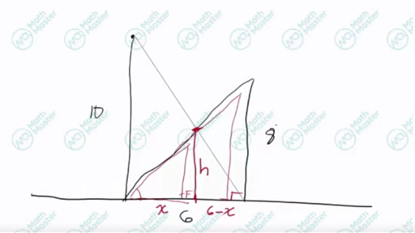
根据图案，我们很容易就能观察到图中形成了两对相似三角形，而它们的边的大小比率是相同。

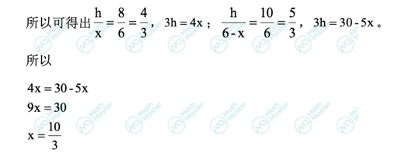
04把它拆分成更简单的问题

应用场景：当你遇到的问题很复杂但能够拆分成几个小问题时，可以选择拆分的方法让计算变得更简单。

例子：Tennessee是美国的一个州名，如果用这个九个字母来组成四个字母的词语，可以有几种组成排列组合？

Tennessee中有许多重复的字母，它有四个e和两个n以及两个t，要知道这个九个字母组成四个字母词语的排列组合是非常困难的。我会选择将其分成更简单的问题，比如分为确定我们要用几个e。

05逆向思考

应用场景：当问题给出的条件很难由表及里推理出结果时，不妨尝试用逆向思考的方式来解决题目。

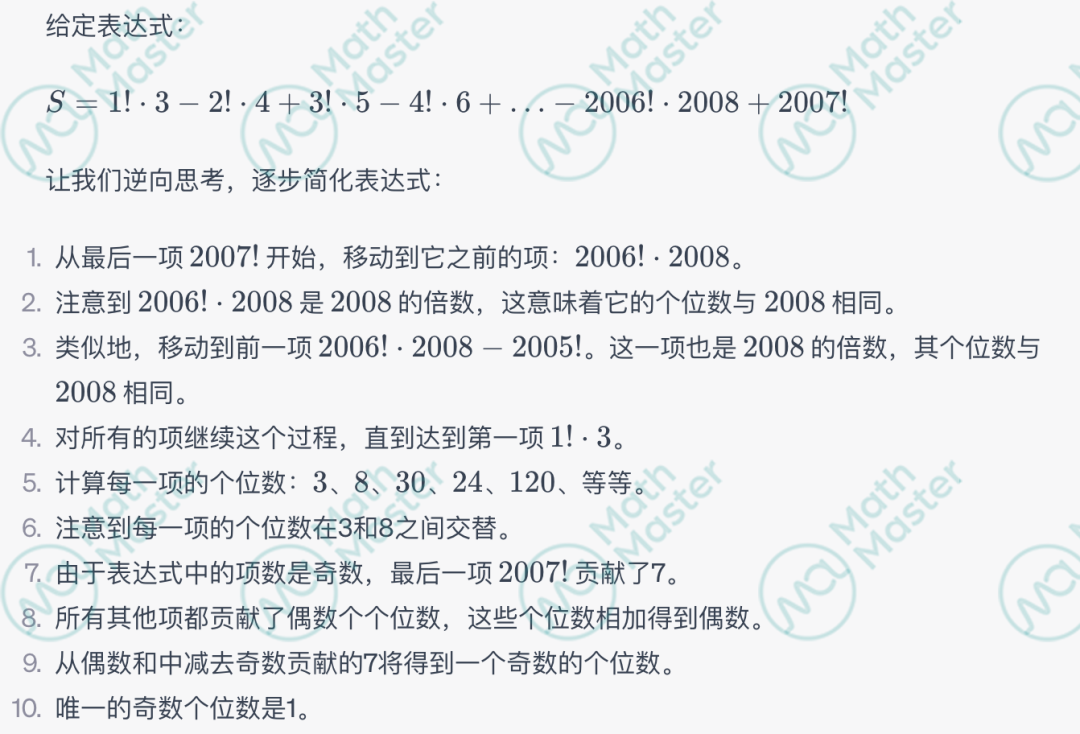
例子：Find the value of the expression S = 1!·3 - 21·4+3!·5 - 4!·6 + ... - 2006!·2008 + 2007!

06寻找矛盾点

应用场景：如果你想证明某事是真的时，可以假设它不是真的，然后寻找“真”与“假”其中的矛盾点，而这正是你解题的关键。

例子：证明圆的半径与圆上一点的切线垂直。

我们可以假设圆的半径与圆上一点的切线不垂直，沿着这个思路就可以证明。

07将你所知道的一切写下来

应用场景：“将你所知道的一切写下来“并不是指要写下早餐吃了什么、写下所有亲戚的名字……而是指当你解题进行不下去时，可以试着把与题目信息有关内容都写下来，比如所有相关定理和公式。

例子：The triangle in the following diagram is drawn over five equally-spaced parallel lines such that the base of the triangle is on one of the lines, and the areas of the two shaded regions are 8 and 20. Find the area of the entire triangle.

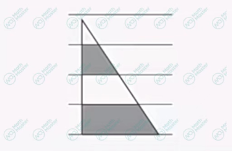
观察完题目后，我们可以看到的是一个大三角形和一些类似的小三角形以及一些等距平行线，将两个阴影部分的面积8和20写上去。

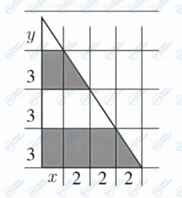
继续观察图形，我们可以试着在这些平行线与大三角形的交点上画垂直线，如下图所示。通过将图形分割成若干个相等的矩形和相等的三角形，观察到下面的阴影部分比上面的阴影部分多出了两个小矩形，说明这两个小矩形的面积为两个阴影部分面积之差，即12，则每个小矩形面积为6，长和宽应为2和3，再把我们所知道的所有信息写在图上，就可以清晰地求出答案。

在讲座的尾声，Dr. Kane贴心地为同学们解答在竞赛中遇到的困惑。

针对同学们认为AMC8题目较难的问题，Dr. Kane告诉同学们，AMC 网站已经列出了每项竞赛的主题框架，应该多关注竞赛的主题。

“掌握主题内包含的基础知识的重要成果，并且形成一定的逻辑思维会对你们解题很有帮助。”Dr. Kane说道，“因为他们不会指望你能用大量复杂的公式去解题，他们可能更希望你注意竞赛主题下题目出现的新模式，然后运用逻辑思维得出答案。”

“多做竞赛题非常重要，你做得越多经验就越丰富，对自己的不足也越了解，也更清楚自己该选择什么样的策略。”Dr. Kane建议道。

讲座最后，Dr. Kane真诚地祝愿同学们能真正享受MathMaster夏令营。“数学是有趣的。有些同学可能没在竞赛中取得优异的成绩，但不要对自己产生怀疑，很多优秀的数学家也在竞赛中表现不佳，甚至从未尝试过竞赛。”Dr. Kane笑道，“要相信自己，你依旧可以成为出色的数学家。”