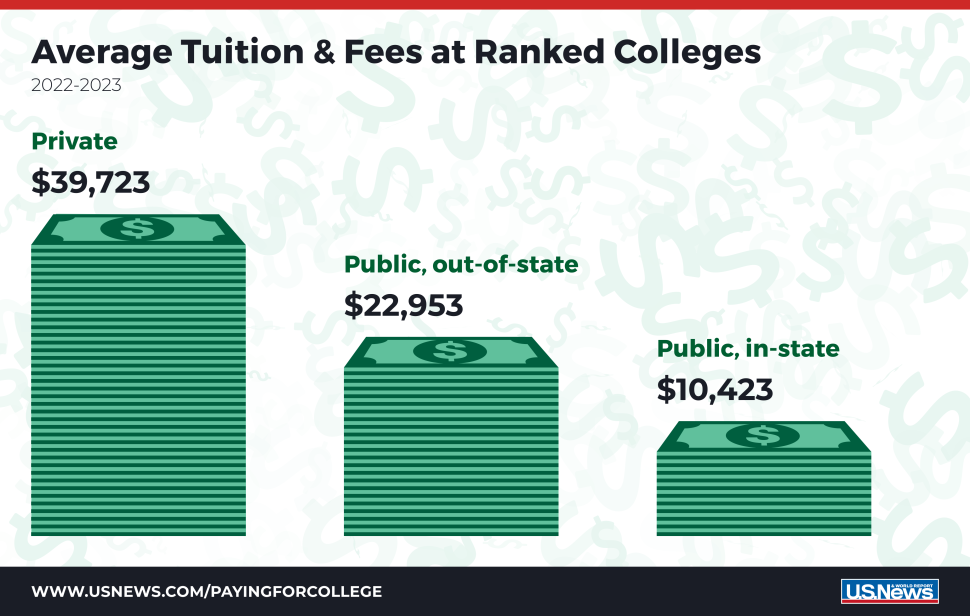
牛剑面试向来以“难度大”著称,尤其是数学专业,“无厘头、很奇葩”的特色都是出了名的,牛剑作为英国乃至世界的Top学府,从来都不走寻常路。
你从PS到笔试一路过关斩将,可能恰恰就倒在面试上。面试作为进入梦想学府的最后一道关卡,千万不能掉以轻心。
了解面试官的提问方式和内容方向,掌握相应的面试技巧,才是冲击牛剑数学系的正确打开方式√。
那么,牛剑数学专业面试都提过什么样的问题呢?下面是真题放送👇
上下滑动阅览
*Past admissions interview questions for Mathematics
* There's a torus/ring doughnut shaped space station with 2 spacemen on a spacewalk standing diametrically oppositie each other. Can then ask a variety of questions such as if spaceman A wants to throw a spanner to spaceman B, what angle and speed should they choose (stating any assumptions made, e.g. that gravity = 0)? (submitted by Oxford university applicant) Comments
* Show that if n is an integer, n^3 - n is divisible by 6. (Submitted by Oxford Applicant) Comments
* Differentiate x^x, then sketch it. (submitted by Oxford university applicant)
* An ant starts at one vertex of a solid cube with side of unity length. caculate the distance of hte shortest route the ant can take to the furthest vertex from the starting point. (answers in this book)
* A telephone company has run a very long telephone cable all the way round the middle of the earth. Assuming the Earth to be a sphere, and without recourse to pen and paper, estimate how much additional cable would be required to raise the telephone cable to the top of the 10m tall telephone poles (answers in this book)
* a thin hoop of diameter d is thrown on to an infinitely large chessboard with squares of side L. what is the chance of the hoop enclosing two colours? (answers in this book)
* an infinitely large floor is tiles with regular hexagonal tiles of side L. Different colours of tiles are used so that no two tiles of the same colour touch. A hoop of diameter d i thrown onto the tiles. What is the chance of the hoop enclosing more than one colour? (answers in this book)
* what is the volume of the largest cube that fits entirely within a sphere of unity volume? (answers in this book)
* what is the area if an n-sided regular polygon inscribed within a circle of radius r? (answers in this book)
* for a circle inscribed in inside a regular n-sided polygon, what is the minimum n so that the ratio of the area of part outside the circle to the area of the circle is less than or equals to 1/1000? (answers in this book)
* give a vector proof that for a triangle inscribed within a semicircle, the included angle is always pi/2 (answers in this book)
* Is it possible to cover a chess-board with dominoes, when two corner squares have been removed from the chessboard and they are (a) adjacent corners, or conversely, (b) diagonally opposite. (submitted by Oxford university applicant)
* Integrate 1/(x^2) between -1 and 1. Describe any difficulties in doing this? (submitted by Oxford applicant)
* If a cannon is pointed straight at a monkey in a tree, and the monkey lets go and falls towards the ground at the same instant the cannon is fired, will the monkey be hit? Describe any assumptions you make. (submitted by applicant)
* Integrate xlog(x). (submitted by Oxford applicant)
* How many solutions to kx=e^x for different values of k?
* Prove by contradiction that when z^2 = x^2 + y^2 has whole number solutions that x and y cannot both be odd. (The Student Room)
* Sketch y=ln(x) explaining its shape. (The Student Room)
* Compare the integrals between the values e and 1: a) int[ln(x^2)]dx; b) int[(lnx)^2]dx and c) int[lnx]dx. Which is largest?. (The Student Room)
* Sketch y=(lnx)/x. (The Student Room)
* Differentiate x^x and (x^0.5)^(x^0.5). (The Student Room)
* Sketch y=cos(1/x). (The Student Room)
* What is the square root of i?
* If each face of a cube is coloured with one of 6 different colours, how many ways can it be done? (The Student Room)
* If you have n non-parallel lines in a plane, how many points of intersection are there? (The Student Room)
* Observation about (6 - (37^0.5))^20 being very small. (The Student Room)
*By considering (6 + (37^0.5))^20 + previous expression, show this second expression is very close to an integer. (The Student Room)
* Sketch Y = (x^4 - 7x^2 + 12)/(x^4 - 4x^2 +4). (The Student Room)
* Sketch y^2 = x^3 - x. (The Student Room)
* Integrate from 0 to infinity the following: Int[xe^(-x^2)]dx and Int[(x^3)e^(-x^2)]dx. (The Student Room)
* If you could have half an hour with any mathematician past or present, who would it be? (Oxbridge Applications)
* Integrate arctan x! (Cambridge applicant, The Student Room)
* Do you know where the multiplication sign came from (Oxford university applicant, mathematics and statistics, The Student Room)
* If we have 25 people, what is the likelihood that at least one of them is born each month of the year? (Oxford applicant, The Student Room)
* What makes a tennis ball spin as it's travelling through the air? (Oxford applicant, The Student Room)
* If (cos(x))^2 = 2sin(a), what are the intervals of values of a in the interval 0 ≤ a ≤ pi so that this equation has a solution? (submitted by Oxford applicant)
* If a round table has n people sitting around it, what is the probability of person A sitting exactly k seats away from person B? (submitted by Oxford applicant)
* You are given that y = t^t and x = cost. What is the value of dy/dx? (submitted by Oxford applicant)
* Differentiate y = x with respect to x^2? (submitted by Oxford applicant)
* Prove by contradiction that 2(a)^2 - b^2 is true only if a and b are both odd? (submitted by Oxford applicant)
* if your friends were here now instead of you, what would they say about you? (Cambridge interview, The Student Room)
* Whatever got you into pole dancing? (Cambridge university interview, The Student Room)
* Why do you play table tennis? (Cambridge university interview, The Student Room)
* Do you know where the multiplication sign came from?
* What is the significance of prime numbers?
* Imagine a ladder leaning against a vertical wall with its feet on hte groun. The middle rung of the ladder has been painted a differnt colour on the side, so that we can see it when we look at the ladder from side on. What shape does that middle rung trace out as the ladder falls to the floor?
* Determine all pairs (m, n) of positive integers satisfying: (a) two of the digits of m are the same as the corresponding digits of n, while the other digit of m is 1 less than the corresponding digit of n (as in, say, 263 and 273); (b) both m and n are three-digit squares. A typical hint from the tutor would be to consider this case for 3 digit pairs (m,n) that is, Find as efficiently as possible all pairs (m,n) of positive integers satisfying the following two conditions: (a) two of the digits of m are the same as the corresponding digits of n, while the other two digits of m are both 1 less than the corresponding digits of n (b) both m and n are four-digit squares. (submitted by oxford university applicant)
* Show that no number in the sequence 11,111,1111,11111... is a perfect square (submitted by oxford applicant)
以上是牛剑的面试曾提过的问题,这些问题大多没有标准答案。
比如:蚂蚁从边长为一的立方体的一个顶点开始。计算蚂蚁从起点到最远顶点的最短路径的距离。
这类问题很考验逻辑思维和空间想象力。
比如:素数的意义是什么?
这类问题则问得非常的空泛,没有一个标准的答案。
比如:你知道乘法符号是从哪里来的吗?
这类问题则需要学生有广泛的知识积累和阅读。
光答出来也不行,牛剑的面试形式是围绕一个话题,由浅入深地讨论。
面试官会根据面试学生的回答追加问题,增加难度。不过别害怕,面试的目的不是要难倒你,而是看你对数学的好奇心、知识和热情。
想要在面试中脱颖而出,不仅要答出问题的表面,还要吃透其中包含的数学原理。

为此,要通过牛剑数学专业面试,以下几点技巧和细节或许对你有帮助:
01、打开思维模式
数学问题可能有正确且唯一的答案,但牛剑数学专业的面试通常没有确切答案,面试官会提出和数学有关的一切问题,先从一个相当简单的基础问题入手,逐步深入到很难的部分。
而答案通常需要你有创造性和批判性思维,以及良好的态度和数学专业知识的坚实基础,能不能答对不重要,答得好答得妙很重要。
在回答问题时不要用固定的思维方式来思考,平时多积累数学知识,看数学相关书籍,时刻牢记打开思维模式的开关,多角度思考,不能固化思考问题。
02、展示思考过程
数学专业面试是非常学术硬核的,在面试对话过程中,面试官一般都很温和的提问,他们会指出错误、提供提示和引出问题,或者延伸问题来回应你的回答。
但这不代表你可以愣在那等待对方抛问题,你可以将数学专业的面试当成是一次学术讨论,回答数学问题时,你只需要大声说出你的想法,向面试官展示你的思考过程。
说出思考过程很重要,面试官不期望你能立刻回答每个问题,而是想看你能否用自信、智慧和清晰的方式来探索和解决未知的问题。如果你沉默不语,他们就无法判断你的能力!
03、不要逃避问题
如果你发现问题很困难,无法立即答出来,你可以告诉面试官,“我从来没有见过这样的问题”或者“我们学校还没有学过这个”,但不要以此为借口逃避回答。这是你展示你渴望接受新想法的机会,所以用“但是让我看看能不能想出办法!”是更好的表达方式。
不要害怕答案的对错,数学专业的面试问题肯定是有一定难度的,所以当你不能马上知道答案时,不要惊慌,告诉面试官你所知道的,提出一些想法,谈谈你解决类似问题的方法。
04、活用表达方式
当面试官提出了一道难题,你可以直接拿出纸和笔演算,直接展示你所有的解答步骤,图文和语言并用的方式来阐述你的思想过程是一个非常好的方法,不仅可以帮助你自己思考,可以让面试官清晰的看到你的思路。
虽然是数学专业的面试,但你也需要用英文来表达,了解西方的一些英语表达模式也是活用表达方式,增强面试沟通的一种手段。
05、强调对数学的热爱
你的热爱和乐趣所在才是学习数学的最好敲门砖,在面试过程中,不要吝啬表达自己内心对数学专业的热爱和看法,要让面试官知道你学习数学的热情,心怀热爱,才会想要进牛剑数学系并为此奋斗学习。
你可以举例说明你的课余时间如何通过在线课程和独立阅读来学习数学。你也可以说明你在数学学习过程中有何种发现和思考,如果你不知道从哪里开始,找一些数学书籍书拓展思维,如《数学万花筒》、《数字之美》等。
05、临场应变能力
在准备面试的过程中,你可以通过牛剑面试题来模拟练习,想象自己是在一个真实的面试场景中,让你的亲戚朋友向你提问,这样你就可以锻炼在时间压力下思考和说话的技能。