今天我们来聊聊数论部分。
数论是数学的重要组成部分,也是 AMC 考试中的核心部分之一。
虽然 “数论” 这个词听上去高深莫测,其实我们从中学甚至小学就已经开始接触数论的知识了。例如,质数的概念,求解最大公约数,最小公倍数等。
AMC 10 中关于数论的题目不仅涵盖了了中学课内所学的知识,还有很多需要记忆的公式定理。同时 AMC 10 涉及到数论的题,往往是难题中的压轴题。
数论类型的题经常出现在考试中的最后两题。那么今天我们就来总结下 AMC 10 中涉及的数论部分的公式定理。
1.孙子定理(Chinese Remainder Theorem)
2.费马小定理(Fermat's Little Theorem)
3 威尔逊定理 (Wilson's Theorem)
4 欧几里德算法 (Euclidean Algorithm)
5 立方和公式(Nicomachus's Theorem)
1孙子定理(Chinese Remainder Theorem)
这是一个为数不多的在西方数学发展史中用东方名字去命名的定理。孙子定理解决的是一次线性同余方程问题。
最早记载于 《孙子算经》中,原文如下:“有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?”
简单地说就是根据不同除数得到的余数,求解满足条件数字的问题。关于此定理的具体叙述如下:

此定理经常用于 AMC 10 和余数相关的题目。
AMC 10B 2017 Q23 (答案见最后)

2费马小定理(Fermat's Little Theorem)
费马小定理是一个在数论问题中频繁被使用的定理。尤其是对于备考 AMC 10 的同学来说,此定理可以求解大部分和指数表达式相关的余数问题。
定理的叙述如下:

同时也伴随这一个推论:
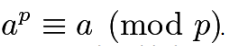
下面我们来看一下如何在例题中使用费马小定理。
AMC 10B 2017 Q14 (答案见最后)
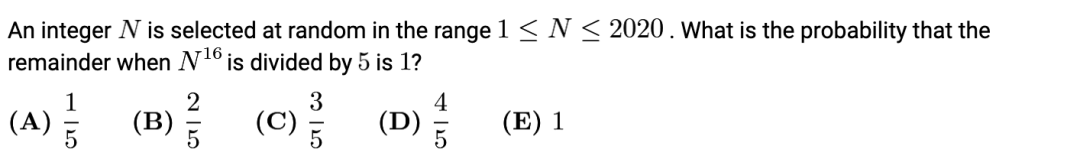
3威尔逊定理(Wilson's Theorem)
这也是在 AMC 10 的考试中出现过的一个和求余数相关的定理。也可以用来判断一个自然数是否是质数。
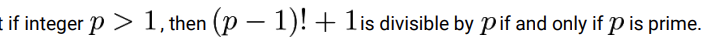
AMC 10A 2019 Q25 (答案见最后)
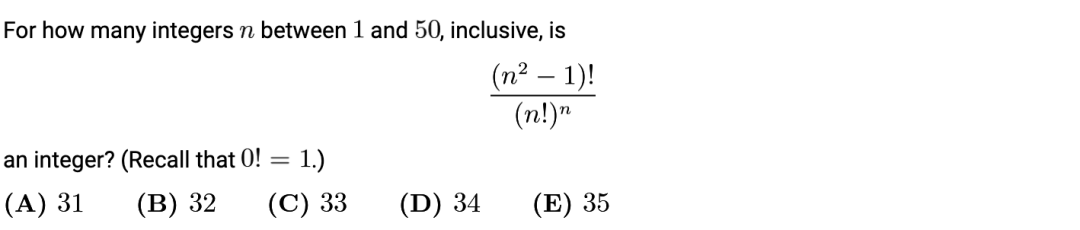
4欧几里德算法(Euclidean Algorithm)
欧几里德算法又叫做辗转相除法,是用来计算两个整数之间最大公约数的方法。
其核心思想是,两数相除得到的余数与其中任意一个数的最大公约数等于原本两个数的最大公约数。该算法的逆过程经常被用来推算一些数的最大公约数。
整个算法流程具体如下:

AMC 10A 2020 Q24 (答案见最后)

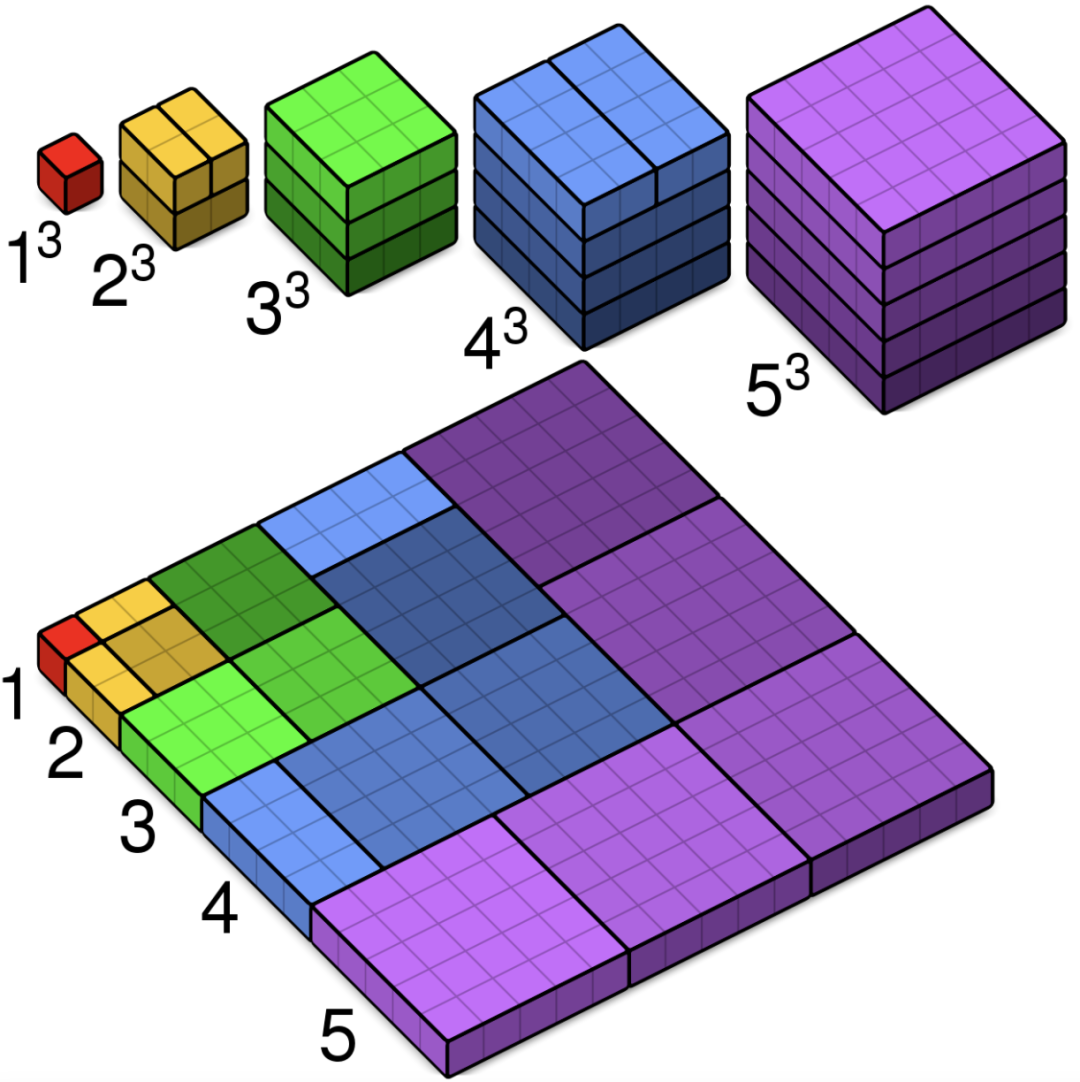
5立方和公式(Nicomachus's Theorem)
这个定理是可以被可视化证明的。从 1 开始的连续正整数的立方和等于对应几个正整数和的平方。
虽然可以使用的机会很少,在特定题目中使用该定理,还是会大大简化求解过程。
AMC 10B 2018 Q16 (答案见最后)
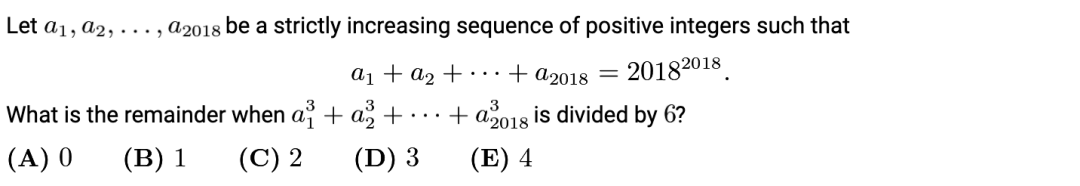
答案与解析