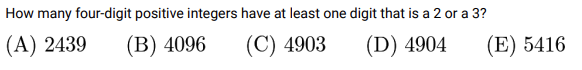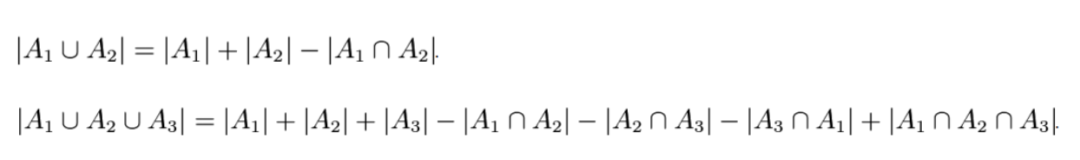今天要开始分享的是 AMC 10/12 必学定理的最后一一个板块:计数。
计数问题在 AMC 的考试中主要分为组合数学 (Combinatorics) 和概率 (Probability)。
简单的排列组合的计算公式相信同学们都不陌生,然而竞赛中的组合问题不仅需要基本的公式,还需要合理的分类讨论以及计数思想。
计数类问题还可以衍生出不同类别的概率问题,其中的核心部分也是计算代表分子、分母的情况个数。
如何有效地 “数”, 如何 “数” 对,今天我们来介绍下在 AMC 10 中计数部分,有哪些重要的计数思想和公式需要我们掌握。
1.互补计数(Complementary Counting)
2.容斥原理(Principle of Inclusion-Exclusion)
3 可分辨性与“隔板法” (Distinguishability)
4 鸽巢原理 (Pigeonhole Principle)
1互补计数(Complementary Counting)
互补计数,顾名思义就是计算所求集合中补集的元素个数。典型的例子是找出 “至少有 n 个” 的互补情况,也就是 “至多有 n-1”。
结合题目中出现的 "至多"、“至少” 这样的关键词,利用互补的思想,可以使一些计数和概率计算变得更简洁有效。
例如下面这样一道例题,AMC 10A 2006 Q21 (答案见最后)
2、容斥原理(Principle of Inclusion-Exclusion)
容斥原理是另一个计数问题中常见的集合原理。
通常使用容斥原理可以计算两个或者多个不同的类别重叠部分元素的个数。它的集合表达式如下,一般来说只需要掌握两集合,三集合对应的结论就可以了。
下面这道例题,同学们可以试试使用给出的集合公式找出答案。
AMC 10B 2017 Q13 (答案见最后)
3可分辨性(Distinguishability)
这个术语看着有些陌生,其实我们在学习初级的排列组合时就已经涉及了可分辨性的这一特征。
排列 (permuation) 和组合 (combination) 的区别就在于前者每个元素是不同的,放入的分组顺序也是可辨的 (distinguishable),后者虽然每个元素不同,但是选出的分组是不可辨的(indistinguishable)。
可辨性最好的应用就是“隔板法”,关于隔板法的问题可以描述为将 n 个元素分为 k 组 或者 k 个非负变量之和等于整数 n。
实际上解决这样的问题只需要先保证每组至少分得 1 个,再添加 k-1 个隔板就可以了。所以对应的公式就是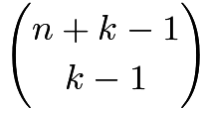 。
。
首先我们来看一道,与 “隔板法” 相关的概率问题。
AMC 10A 2018 Q11 (答案见最后)
“隔板法” 还能用在一些代数问题上,不知道下面这道题有没有给你一些使用 “隔板法”的启发。
AMC 10A 2016 Q20 (答案见最后)
4鸽巢原理(Pigeonhole Principle)
鸽巢原理也叫抽屉原理,简单的解释为 n+1 个元素分成 n 组,至少有一组包含两个元素。又或者为什么一个学校里,一定有两个同学的生日是同一天呢?因为生日只有 366 种,而学校的人数一定大于 366, 所以一定有人的生日相同。
简单易懂的原理,应用时也可以解决大问题。
AMC 10A 2006 Q20 (答案见最后)
答案与解析