回顾五月赛季,P4模块在题量上虽有减少,不过难度上的确有所提升,同时数学模块作为 2023年最受欢迎的 5大 Alevel科目之一,分数线的上浮也是必然的。下周即是十月赛季的 P4统考,本篇将由理综教研部老师就近年题型与考点入手,为大家做最后的冲刺指引。
历年题型
考点侧重
『化简与求导』
以下将以 2023年 5月的 P4真题卷为参照,对比近年来题型设置与考点分布。首先是二项展开式,需注意标准形式的三点 ①“1” ②指数是负数,分数 ③ x展开的有效范围。
2023年 5月卷中直接给出二项展开式,根据展开规则完成即可;2023年 1月倦中的二项展开式则是结合 Partial Fraction出题;2022年 10月卷的二项展开式是给出分式根号的形式,需先化简成标准形式,再展开。
这一知识点的题型,需要考生更加敏感,有时题干给出的标准形式或者类似标准形式,部分考生还能想起来。而写成分数形式,或是根号形式时,同样不可忘记将二项展开式的知识点与之相联系。

来源:2023年 5月卷 P4真题
而对于隐函数求导,一般多结合乘法的求导法则,个别会结合除法的求导法则,还需多熟练带指数函数的隐函数求导。用隐函数的求导原则推导指数函数的求导公式是至关重要的,教材附有例题,并有在真题中单独考核过。理综教研部温馨提示:谨记导数是切线的斜率。该考点的题目还将求切线,法线与交点进行了融合。

来源:2022年 10月卷 P4真题
参数求导会多一步将参数求导转化成笛卡尔求导的过程,此处需注意参数求导需结合链式法则,以及
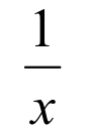
的求导和积分,仔细审题。2023年 5月卷中参数求导放在了第八题,但参数求导占 5分,旋转体积占 7分。2023年 1月卷则是包含了三角函数的参数求导,需应用链式法则。2022年 10月卷的参数求导放在了第一题,比较单纯的考察参数求导,并未与其他知识点结合。
『三大积分方法』

来源:2023年 1月卷 P4真题
关于 Partial Fraction积分,在使用该方法前,需重点检查是否需要大除法,切不可一开始就 Partial Fraction积分。2023年 6月卷和 2022年 10月卷都有考一题,2023年 1月卷则是单独出题。但会在别的题目的积分运算中,并未提示需用 Partial Fraction积分,但根据被积函数的形式,需选择用 Partial Fraction积分。

来源:理综教研部模拟作答过程图
在以上模拟作答中,该考生的 Partial Fraction没有问题,但积分时忘记积分公式,没有乘上前面系数的倒数,造成 b问扣一分。此类错误很容易被忽视,每一行都是正确的,A和 B算的结果也是对的,但最后一行总结时抄写错误,扣去一分,考试还需稳住心态。若下面的小问该考生继续沿用了这个错误的结论,则会失去更多分数。
而换元积分,基本是在积分相同类型函数相乘,或带分式,带根号的情况下使用。需牢记换元积分的一般步骤:换被积变量、换被积函数以及换被积区间。三个由换元积分推导出来的公式需要考生熟练敏感,有助于后续高等数学的学习。
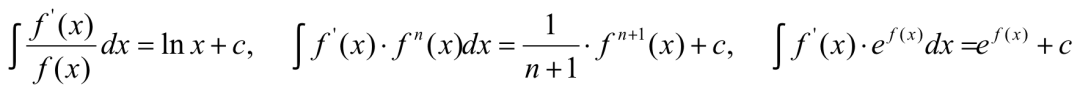
来源:理综教研部整合换元积分步骤
分部积分 By Part用于积分不同类型的函数相乘,有时可能一次分部积分积不出来,则需多次。或第一步分部积分,第二步换元积分。切不可一次积分未果,就轻言放弃。
2023年 5月卷将分部积分与换元积分放在了一题,第一问中分部积分涉及 4分,第二问则是 6分的换元积分。2022年 10月卷中换元积分一大题,分部积分作为计算过程涉及 9分。2022年 10月卷也是分部积分和换元积分放在了一题,第一问分部积分 7分,第二问换元积分为 5分。
部分考生不重视换元积分,平时练习不够,造成整体方法理解上虽快,但细节出现了遗漏,造成一整道题目写不完整。下面对照模拟作答看下 2023年换元积分的模拟作答。

来源:理综教研部模拟作答过程图
这两位考生忘记了等号两边可同时对 x求导,一直尝试 x用表示 u。有些形式简单,可直接表示。有些相对复杂的则只能等号两边同时对 x求导,应用链式法则。此处需引起高度重视。
涉及到这三种积分方法的知识点还有参数积分,旋转体积积分 (需谨记公式),解微分方程 (关于微分方程,特别注意 rate是关于时间的求导,题干较长,读题需仔细,及时将文字转化成表达式)。即使附加上题干中的实际背景,本质上还是积分运算。由于积分所占比重之大,扎实掌握下来,P4模块的大块分值也能收入囊中。

来源:理综教研部模拟作答过程图
旋转体积注意旋转的曲线是几段,是否需要分段积分。其中 d问有 7分的高分值,不过该考生只对直线进行了积分,仅得 1分。注意还有一部分曲线下方的区域旋转,所以还要对一部分曲线进行积分。
但曲线的笛卡尔表达式还未知,所以还需把参数函数转化成笛卡尔函数,再积分。参数函数转化成笛卡尔形式+旋转体积积分,这个题目格调都高了。P4的试卷在考察 P4的知识点时,对综合知识点的题型很舍得给分。
『向量与反证』
向量涉及知识点较少,一方面是向量的点乘计算公式,另一方面是直线的向量表达形式,包括三角形法则。其他两点之前距离公式,中点坐标公式都是基础段的内容,会参杂在向量题型之中。另外需明确直线夹角与向量夹角的区别。

来源:2023年 6月卷 P4真题
反证法涉及考点可分为以下四点:①证明无理数 ②证明如果 a是谁的倍数,则 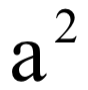 也是它的倍数 ③利用整数推出矛盾 ④找错。具体例题都可在教材第一章节中找到,内容相对基础,不容失分。
也是它的倍数 ③利用整数推出矛盾 ④找错。具体例题都可在教材第一章节中找到,内容相对基础,不容失分。

来源:2023年 1月卷 P4真题
以上就是理综教研部根据近年 P4模块真题设置与考点侧重的整合梳理,复习规划需要注意主次分配,搭配教材与错题整理高效筛查是为关键。预祝各位在下周的统考中能够赛出水平,摘星成功!












