Cosmic Velocities and Schwarzschild radius (宇宙速度和史瓦西半径)

先提一下：航天发射一般都是自西向东（跟地球自转方向相同）发射的，因为地球自西向东自转，可以利用自转的这个初速度，节约能源。

本文在需要的地方都不计空气阻力、把地球看成均匀球体、并把中央天体看成静止。

各个天体其实都可以有宇宙速度 (cosmic velocities), 但因为一般来说涉及到的是从地球发射航天器，所以我们先讲地球的情况。从其他天体发射的情况，公式推导方式类似，但数据会不同。AP 物理涉及到的宇宙速度一般是第一、第二宇宙速度。

a)第一宇宙速度 (the First Cosmic Velocity)

第一宇宙速度 (the first cosmic velocity) 也叫地球的轨道速度 (orbital speed), 是航天发射所需要的最小速度。

从平抛石头的故事开始说起。人为同样高度平抛扔出去的石头，速度越大，石头落地离起始点越远。但因为人为扔的速度不够高，石头总是会落回到地球上。因为地球是球形的，理论上石头速度足够大的时候，石头飞到足够远，石头下落高度（下图中 AB）正好是地球大圆曲线下落高度时，是可能绕着地球进行圆周运动的。忽略摩擦力、把地球看成理想的均匀球体时，这个刚好沿着地球表面飞一圈的速度就是第一宇宙速度。

理论上以第一宇宙速度发射的航天器恰好可以沿着地球表面航天飞行（但在大气层外、没有摩擦力）。

第一宇宙速度的计算方法还是在地表万有引力提供向心力：如下（有些物理量还会出现在本文后续推导中）。

其实，第一宇宙速度的公式应该很熟悉了。第一宇宙速度的理论值大约是 7.9 km/s. 要航天器发射后不掉回地球，航天器必须加速到第一宇宙速度。当然，一般发射的航天器都是有目的轨道的，具体如何进入目的轨道，涉及到的计算、加速等就更复杂了。

发射速度超过第一宇宙速度（但不到第二宇宙速度）的航天器，才能升到更高的绕地轨道。

航天器在同一个轨道绕行时是不用点火的，而如果是从小圆轨道上升到大圆轨道，要两次加速、中间经历椭圆轨道，见上次的文章《天体运动能量-1》。并且，上次讲过了：虽然在更高圆轨道上的速度低于第一宇宙速度，但是，从地球发射时速度需要超过第一宇宙速度（部分动能会转化为更高圆轨道上的势能）。

。

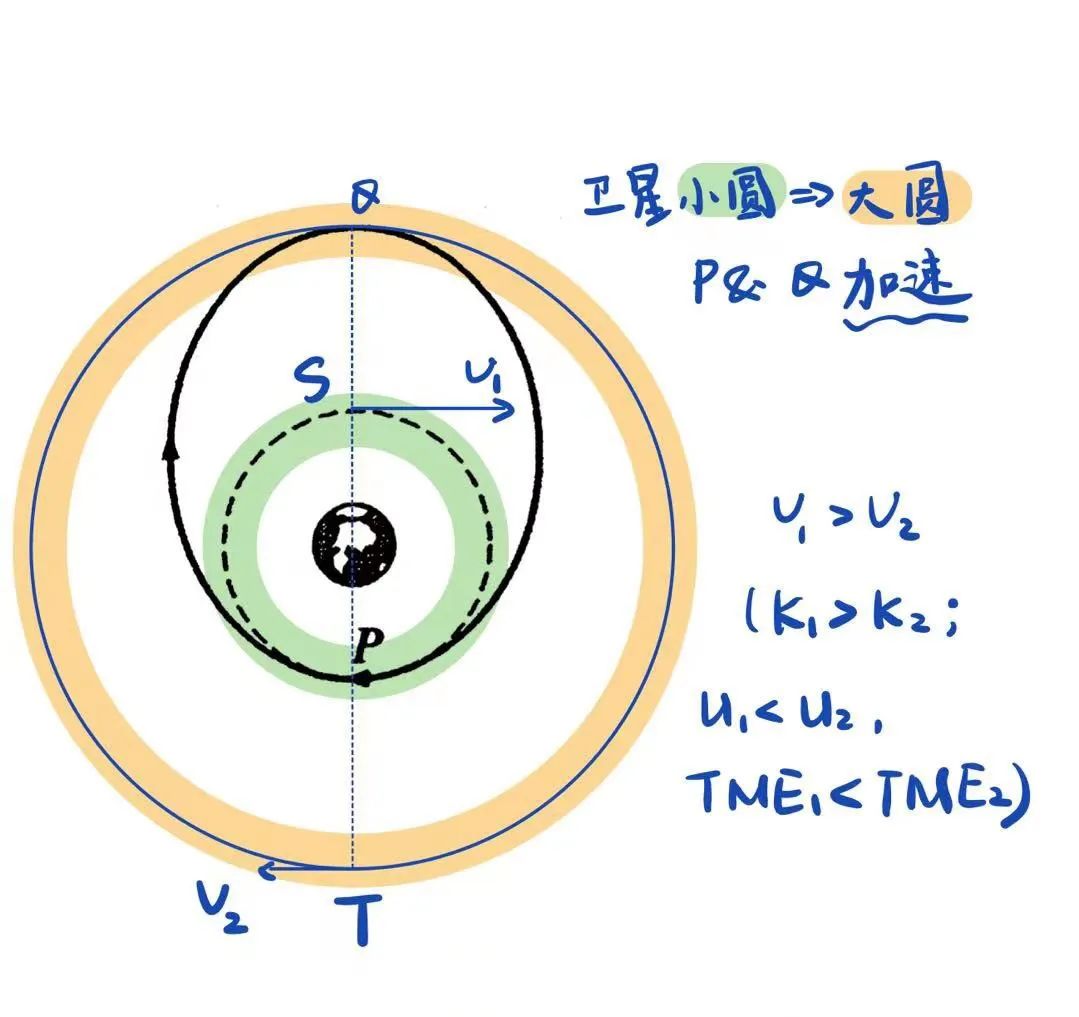
b) 第二宇宙速度 (the Second Cosmic Velocity)

从第二宇宙速度 (the second cosmic velocity) 开始，是地球逃逸速度：从地球出发的航天器，速度超过第二宇宙速度、但不超过第三宇宙速度，就可以逃脱地球的引力、绕太阳运动。

第二宇宙速度的理论公式、计算一般是用机械能守恒 (conservation of mechanical energy) 推导出来的。推导第二宇宙速度时，假设航天器刚好可以飞到离地球无穷远处（飞到无穷远处动能刚好为 0; 无穷远处系统势能也是 0）。推导过程如下。

从推导出的结果来看，第二宇宙速度是第一宇宙速度的√2倍。第二宇宙速度的理论值大约是 11.2 km/s.

接下去的内容 AP 一般不会考，可以不用看下去了。

c)第三宇宙速度 (theThird Cosmic Velocity)

第三宇宙速度 (the third cosmic velocity) 是从地球沿地球绕太阳公转切线防线发射逃出太阳系的卫星需要的最小速度。

第三宇宙速度的推导也用的是机械能守恒，只是中央天体会变成太阳，并且要考虑地球绕着太阳公转的速度。因为 AP 一般不考，就不推导了。第三宇宙速度的理论值是 16.7 km/s, 有兴趣的自己去查一下过程。

d)史瓦西半径 (Schwarzschild Radius) 和黑洞(Black Holes)

既然讲了逃逸速度的公式，忍不住继续说说其他天体的逃逸速度（把第二宇宙速度中质量、半径换成其他中央天体的质量和距离）和黑洞。（并且忍不住想到白 Ice 的沙瀑噩梦，甚至一度觉得醒来后跟白 Ice 说话的“瓦西里”，是“史瓦西半径里”的缩写）

如果一个天体的逃逸速度大于等于真空光速c（人类已知自然界物体运动的最大速度）, 那连光（更不用说其他物质了）都逃不出那个天体的引力范围，这个天体就成黑洞(black hole) 了。逃逸速度正好是光速时的临界半径就是这个物体的史瓦西半径 (Schwarzschild Radius). 如果一个物体半径低于史瓦西半径（一般是巨大的的恒星、中子星等，被非常非常巨大的压力压缩到史瓦西半径以内），它将成为黑洞。黑洞密度极大，能吞噬它的史瓦西半径中所有的光（和其他物质）。

听起来挺玄的，但忽略计算等理论，大家多少也听说过黑洞的密度很大、一般质量很大、能吞噬一定范围内（其实是这个黑洞的史瓦西半径内）的一切物质（包括光）。

再顺带提一下，虽然和考试无关：广义相对论还预测黑洞中心还存在奇点 (singularity, 半径无限接近于 0, 密度无限大的点）。但这个范畴中广义相对论 (the theory of general relativity) 和量子力学 (quantum mechanics) 之间有矛盾。物理学家提出的一些比较新的理论，如弦理论 (the string theory), 一开始就是为了试图解决这两个理论的不兼容性（这个倒是在已经逝去的 SAT subject test 中是个要记的物理学发展史常识）。