👇AMC数学竞赛泄题事件在竞赛圈引发广泛热议

(图源:小红书)
AMC泄题不仅对竞赛的公平性提出了挑战,也给备考生和家长们带来了新的思考。作为爬藤的孩子们比较热衷的竞赛,每年吸引全球超过30万名学生参与,它不仅是评估数学才能的重要平台,更是学生逻辑思维和解题技能的一次重要考验。
相信在此次事件以后,大家也有很多疑问:
- 如何看待AMC的含金量?
- 今年AMC有哪些新趋势?
- 确认晋级AIME该怎么冲刺?
- 计划明年参加AMC怎么规划?
机构将在本文为大家提供超干货的AMC考情总结和规划,想要的答案都在文章里!
请记住,摆平心态,长期规划,轻松迎战变化才是成功的关键。
01、数学竞赛的未来在哪里
泄题事件频发,AMC含金量不再?
考试前,AMC10/12的A卷以模拟卷的名号从AoPS(数学竞赛交流社区)泄露出来,直到考试,官网也并未做出任何调整,近千人拿到了答案。很多家长开始彷徨,如果明年再这样该怎么办?我们有实力的同学需要做些什么?
除了同时参加AMC10/12B卷的考试,争取在AIME获得好成绩外,同学们还可以参加英国的BMO、加拿大欧几里得、澳洲AMC等竞赛来佐证。知识点和考试范围跟AMC都是互通的,准备起来成本也相对较低一些。

另外也想强调,参加竞赛为了辅助升学只是一方面,帮助孩子找到热爱并为之努力也是一种收获。
准备大于天赋,竞赛选拔机制变革?
拿AMC12A的压轴题来说,已经掌握这道题公式的同学,看到题目后立马就会做。不知道的话,通过长时间的推算也能得到答案,但在限时的竞赛里,已经落伍了。

(图源:机构名师讲座)
所以,竞赛早已不是仅靠天赋就能拿下的,更多考察的是知识点掌握的是否全面。这也说明官方在尊重有天赋孩子的基础上,更肯定愿意认真学习的学生。那么2023年AMC 10/12竞赛还透露出了哪些考点规律?
02、2023年AMC 10/12考试新趋势
AMC 10:三角函数“横空出世”
今年AMC10,“三角函数”被列为关键词。为什么呢?
熟悉的同学们应该知道,在一道有多种解法的题目里,作为非考点的【三角函数】,通常被视为解题捷径。AoPS里的解析,也提供过用三角函数的解法。作为非主角的三角函数,在本次考试里不同往常(如下图),压轴题的基本所有解法都需要用到三角函数,而且要做到非常熟练的使用,这道题才可以解出来。
 (图源:机构名师讲座)
(图源:机构名师讲座)
划重点!!!
这道题是跟AMC12共享的压轴题,结合往年的卷子,我们可以看出AMC10在渐渐地融合AMC12的考点。同时也意味着AMC10的考点内容越来越多,建议备考AMC10的同学们能尽可能多的掌握运用知识点和解题技巧!
AMC12:【数论】必须长期积累
本次AMC12的关键词为“数论”。
组合和概率虽然一直是高频考点,但今年却是【数论和相关的代数题】居多。抓住这个信号的学生,很明显你已经赢在了明年考试的起跑线!
但要注意的是,数论在高中教材里涉及的非常少,想拿高分的学生,建议选取一些大学的数论教材,或者适合高中生去学习的大学数论教材,进行系统性学习。另外,纯粹的数论知识是很难通过临场发挥,或者组合知识来解题的,而是需要长期积累。
简而言之,AMC的赛前准备非常重要。大家对传统竞赛(3小时起)的理解,是考学生解决问题的能力,如何拆解问题,进而找到解决的方法。但AMC作为限时竞赛(75分钟),逐渐弱化对该能力的要求,而是需要考生要知道越来越多的东西。它更像一个竞赛里的文科考试,知道的东西越多,准备的越充分,越有可能拿到理想的成绩。
所以再次强调,准备尤为重要!
03、2024年2月AIME如何冲刺
想参加AIME考试的同学请注意,三个月的准备时间,虽然有些仓促,但从现在开始针对性的准备起来,为时不晚!分数预测放在这里供大家参考。
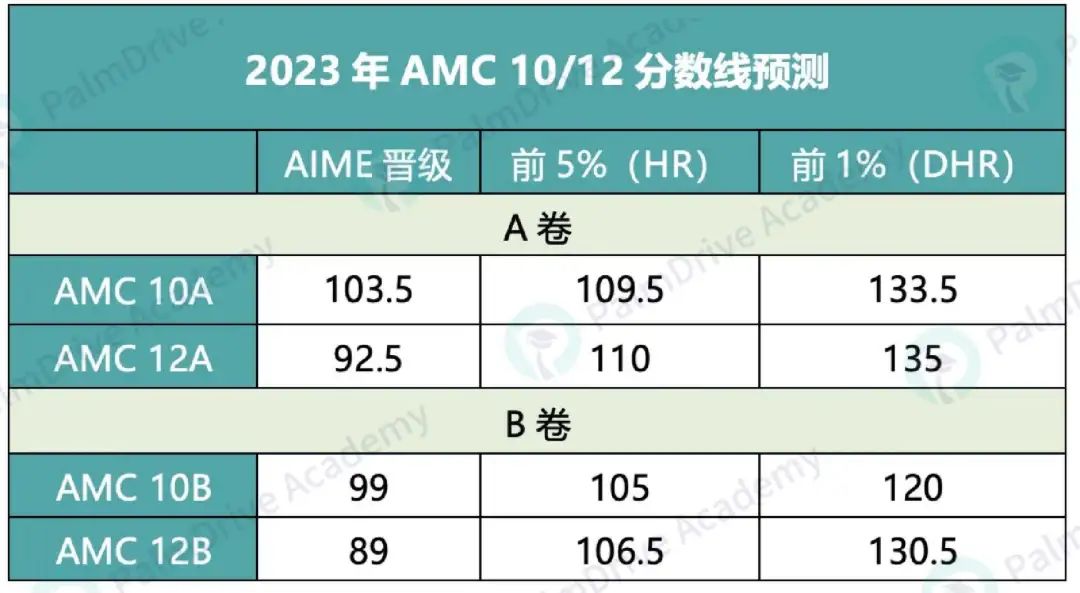
作为理工科学生申请的有力竞争,从AMC选择题到AIME填空题的转变,对计算能力要求变高。时间为3小时,共15题,难度可参考下图。

建议针对自己的预估分数和实际目标情况进行理想分数的设定。
AMC10进阶AIME的同学,建议先把跟AMC12重合的概念和定义掌握好;
AMC12进阶AIME的同学,掌握新知识点后,针对目标分数进行高强度准备。
小贴士
AIME的分数,如果希望对大学申请或者夏校申请有帮助,需要考到7-9分。想进阶USA(J)MO美国数学奥赛,9-10分是安全线,同时也需要参考AMC的权重。
04、2024年11月AMC10/12备考规划
那么如果想明年参加AMC比赛该怎么规划?Jiang老师根据经验为三类备考生提供了非常详细的建议:
1,如果你是AMC10备考生:

2,如果你是AMC10进阶AMC12的新考生:
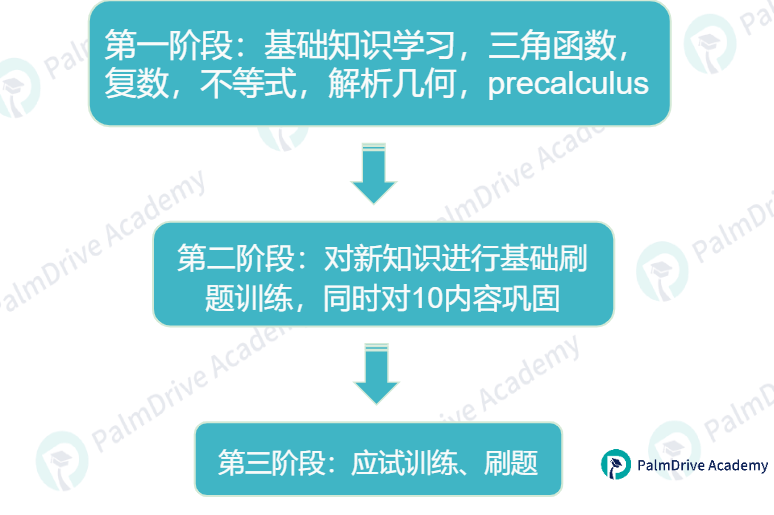
3,如果你曾考过AMC12:
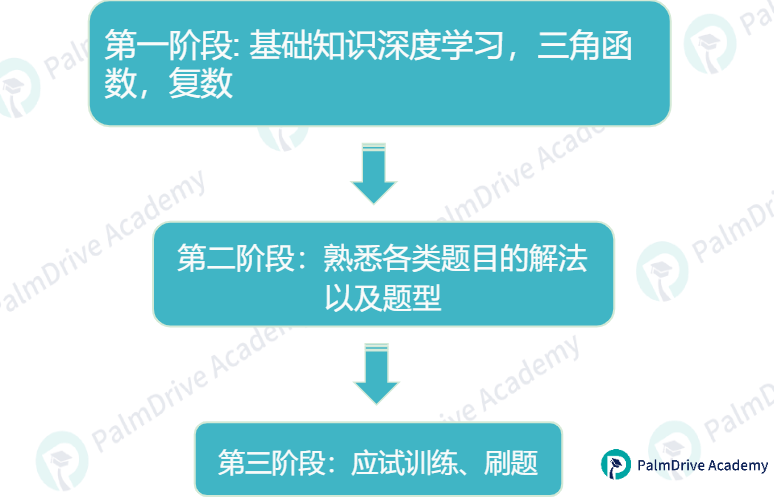
无论你是哪个进程的备考生,第一阶段要放在5、6月前准备完成,其次暑假期间做好第二阶段的任务,再考前进行最后的突击!
看到这里相信你对AMC有了初步的规划和准备,但不得不说的是,AMC准备过程中,不能仅仅依靠课内所学,同时必须要摄取课外知识。
那么在摄取新知识和新定理的过程中,能不能做到很好的理解消化?中途产生的理解偏差是否能立即意识到?有没有在自学数学的过程中,走了弯路,产生了厌学的心理?这些都是过往学生常常出现的状况。
学会知识的有效筛选,把学和练有效结合,而不是死扣概念和定理。灵活的解题思路需要有效的引导,才能游刃有余的解题!