2024年AIME数学邀请赛知识点分布

万众瞩目的AMC10/12终于出分啦！

除了分数查询，考生们关注的另外一大重点就是AIME的晋级线了，晋级分数线预计在12月末左右发布！

北美的AMC辅导教练们给出了预测Cutoff分数线（参考2023年数据）👇

AMC10

AIMEcutoff预估:102

Top 5%：109

Top 1%：121.5-133

AMC12

AIMEcutoff:85.5-90

Top 5%：105-106.5

Top 1%：129

已经查到分数并有望拿到AIME“入场券”的同学们，快打起精神来！留给大家备考AIME的时间已不足70天！

AIME美国数学邀请赛

AIME全称American Invitational Mathematics Examination, 是介于AMC10、AMC12及美国数学奥林匹克比赛（USAMO）之间的一个数学赛事。

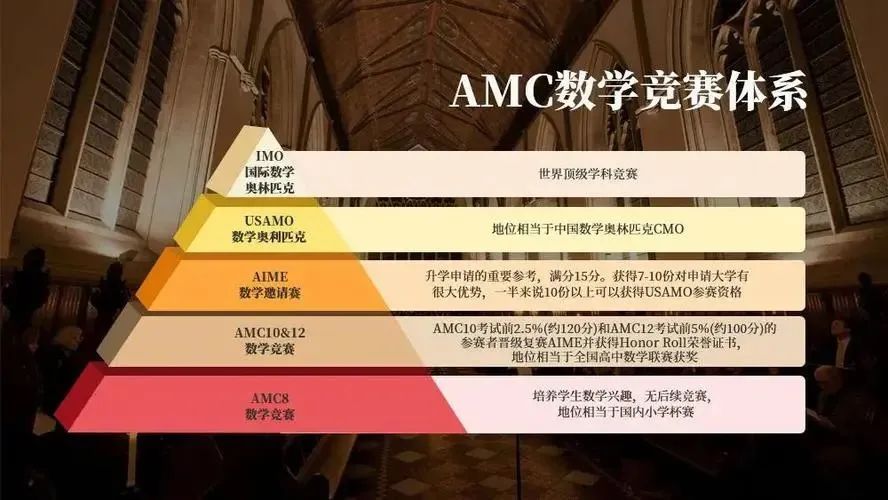
比赛开始于1983年，在每年的3月中旬和三月底举行（2022年跟随AMC10、12考试时间的调整改为每年的2月举行），一共两次，分为AIME I和AIME II，两次考试和AMC 10和12的A和B的考试模式类似，难度和效力相同。

参赛对象

AMC10（*2.5% Distinction）/AMC12（*5% Distinction）优胜者（实际晋级分数会低于Distinction分数，比例也会更高）

AIME考试时间

（I类） 2024年2月1日 ;

（II类）2024年2月7日

考试形式

AIME由15道数学题组成，满分为15分，所有题目的答案为0至999之间的整数，要求考生在3小时内完成。

AIME知识点分布

AIME的考试内容仍然和经典的高中数学竞赛所覆盖的知识框架一样，分为数论、代数、几何和组合四个板块。

每个板块在一些高阶知识点的要求和考察上会较AMC12有进一步提高。

NumberTheory

欧拉定理和中国剩余定理基本一定会在Q11+的数论题目中做考察，且会要求考生对于这两个定理的表述形式、证明逻辑以及应用场景做全面的掌握。而在AMC10以及AMC12中，这两个高阶的数论定理基本上只会做对其背后idea的模糊考察。

另外，和LCM（最小公倍数）还有GCD（最大公约数）相关的题目在AIME中考察相对较少（但确实还是有的），而在AMC10和AMC12中这部分的数论难题还不少。

Algebra

在代数部分，AIME对三角函数的进阶恒等式（如辅助角公式，和差化积以及积化和差等）的变形和处理提出了进一步的要求，对于涉及一个三角形中三个内角的具有对称结构的三角表达式的处理会经常涉及，而这部分内容基本不会在AMC12中出现。

此外，AIME会略微涉及到NewtonSum的递推求解idea（但并不会要求大家掌握最一般的牛顿和递推公式）以及简单的函数方程问题，会涉及更多的研究对称和替换结构的方程组求解的问题，以及更多的极值求解问题。而对其他大部分内容如多项式理论、二次函数理论、对数和复数等知识点的考察深度和AMC12基本一样。

Geometry

AIME的难度主要体现在对计算工具（三角、坐标以及复数）的使用频率及计算量的显著增大上。现在，AIME的题目基本不会专门涉及非常特殊的竞赛几何定理（如梅涅劳斯、塞瓦、托勒密、欧拉定理等），了解这些定理或许可以提供解决部分题目的一些思路，但基本上每道题目都有更加基本的只基于最简单几何性质和几何分析工具应用的解法。

同样，我们再次强调三角在AIME几何题目中的重要性，尤其是中高编号的题目，找到某个关键角，利用和它相关的三角函数以及正、余弦定理建立重要线段之间数量联系是解题的关键。

可以这样说，大家如果不能熟练掌握三角的方法，在AIME10+的几何题目里基本是寸步难行的，这是AMC10进阶到AMC12和AIME在几何部分最大、最重要的点。

Combinatorics

组合部分中，AIME的题目风格和AMC10以及AMC12相差无几，不过会用到递推（recursiveMethod）思想，以及涉及到进阶组合恒等式（Vandermonde等）的题目会显著增多，大家可以针对性练习一下。

👉AIME的Q1-Q5大致对应AMC12的Q15-Q18，难度系数为2.5-3.5，完成这部分需要约5*6=30分钟；

👉AIME的Q6-Q9大致对应AMC12的Q18-Q21，难度系数为3.5-4，完成这部分需要约15*4=60分钟；

👉AIME的Q10-Q12大致对应AMC12的Q21-Q23，难度系数为4-5.5，完成这部分需要约20*3=60分钟；

👉AIME的最后三道压轴题Q13-Q15大致对应AMC12的Q24-Q25，难度系数为5.5-7，平均每道题目需要15分钟-45分钟。

AIME题目难度大、考试时间长，既是对学生数学竞赛题解题技巧、思维水平的考验，同样是对学生耐力的磨练。

因此，对想参加AIME、并在AIME竞赛中取得优秀成绩同学来说，需要提早准备、做好长期训练的规划！