在前几天的文章《袋鼠数学思维挑战活动》中,我选择了袋鼠数学三个LEVEL共9道代表性的题目。本文将给出这9道题的解答并做一些点评。
袋鼠数学每套题都有不同分值的题目,按题目顺序,分值依次是3,4,5分(具体分值请参考《袋鼠数学思维挑战活动》文中的介绍)。随着分值的增加,题目难度也相应地有所提升。通过每个LEVEL的3道不同分值的题目的解答,我们可以体会其中的难度变化。再换个观察角度,通过比较不同LEVEL的同分值题目的解答,我们还可以体会推理的复杂性怎样随着年级的增加而增长。
下面我们就来具体看一下这些题目的解答吧。
LEVEL A
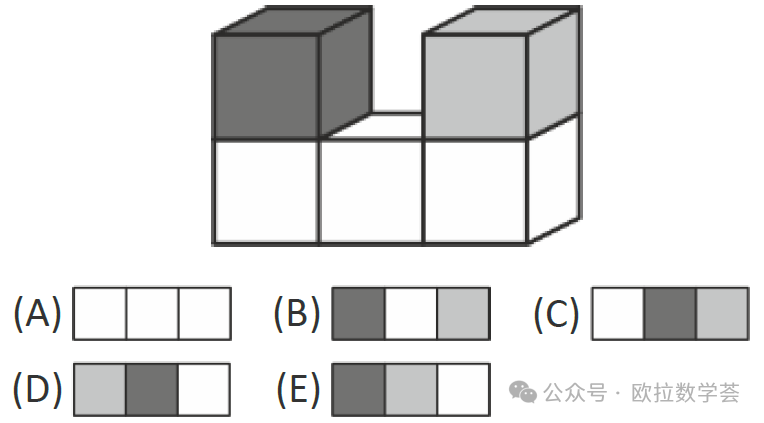
1. 下图是从正面观察5个立方体看到的样子。那么从上方观察会看到什么呢?(3分题)
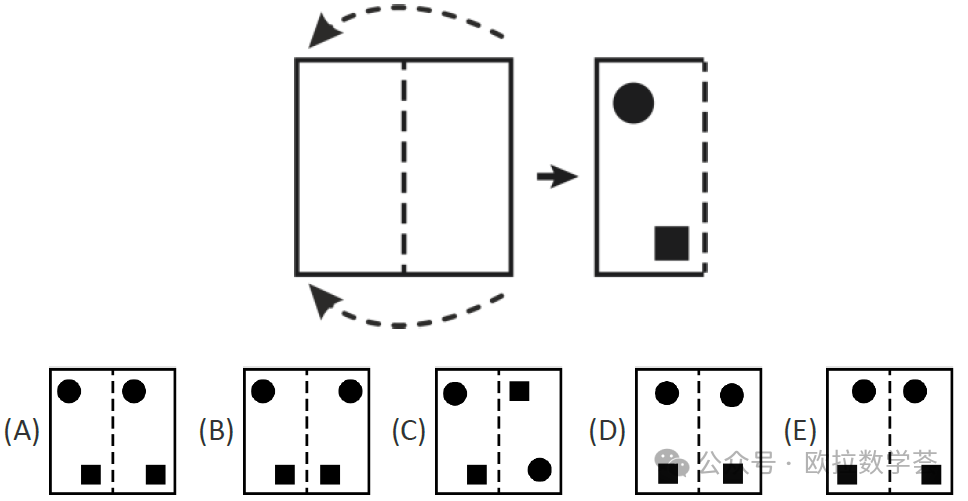
2. 把一张纸对折,然后在纸上打两个孔。把这张纸重新展开后会是什么样子呢?(4分题)
3. 一个池塘里住着三只青蛙。每天晚上都会有一只青蛙唱歌,另外两只青蛙只是听歌而不唱歌。在9个晚上后,第一只青蛙唱了2次歌,第二只青蛙听了5次歌。第三只青蛙听了多少次歌?(5分题)
解答和点评
第1题是图形观察题。从上方应该看到从左到右排列的三个正方形,颜色依次是黑、白、灰。所以答案是(B)。
第2题考查图形的对称关系。在折叠后的纸上打孔,展开后的两个孔应该关于折痕对称。左半侧的两个孔的位置符合题图的是A,B,C三个选项,其中A和C不符合对称关系。所以答案是(B)。
上面这两道图形题跟常识的关系非常紧密。一二年级的孩子应该多接触实物,建立起这些常识观念,再来做这样的题目,而不是为了解题而解题,生硬地给孩子讲解题目。很多优秀的数学启蒙游戏都是以帮助孩子建立这些常识为目的而进行设计的。
第3题是推理题。这道题有多种推理方式。在此仅介绍其中两种。特别提醒一下,你也许认为下面的推理过程不算太复杂,但这对于二年级的小朋友来说已经是很长的逻辑链条了。
解法一:对每只青蛙而言,每个晚上要么在唱歌,要么在听歌。已知第二只青蛙听了5次歌,所以它唱了9-5=4次歌。而第一只青蛙唱了2次歌,所以第三只青蛙唱了9-2-4=3次歌。从而,第三只青蛙听了9-3=6次歌。
解法二:当一只青蛙在听歌时,那个晚上一定是另两只青蛙中的一只在唱歌。已知第二只青蛙听了5次歌,所以第一和第三只青蛙一共唱了5次歌,即第三只青蛙唱了5-2=3次歌。所以第三只青蛙听了9-3=6次歌。LEVEL B
1. 玛丽按照下图所示的时间安排开和关三盏灯。有多少分钟是恰好有两盏灯开着的?(3分题)

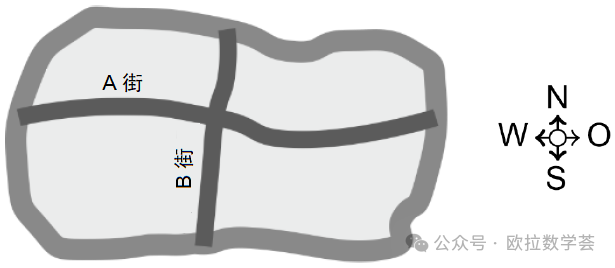
2. 如下图,A街的北侧有7栋房子,B街的东侧有8栋房子,A街的南侧有5栋房子。请问B街的西侧有多少栋房子?(4分题)
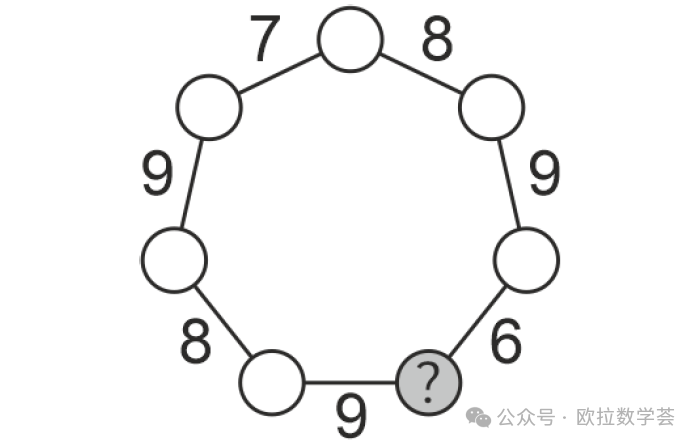
3. 老师在下图的圆圈内分别填入从1到7的数,每个圆圈内填一个数。相邻两个圆圈内的数的和写在两个圆圈的连线旁边,如图所示。打问号的圆圈内填的是哪个数?(5分题)
解答和点评
第1题是图表观察题,只需要数一下有多少个分钟是恰好出现了两条线段的。从图中可以看出,第2, 4, 5, 6, 7, 9, 11, 12分钟都符合要求,一共是8分钟。
第2题是推理题。通过观察街道图,A街的北侧和南侧的房子加起来就是图中所示的区域内的所有房子。所以这个区域内一共有5+7=12栋房子。类似地,B街东侧和西侧的房子加起来也是区域内的所有房子。而已知B街东侧有8栋房子,所以B街西侧有12-8=4栋房子。
第3题仍然是推理题,并且与第2题一样,都需要结合对图的观察来展开推理。当推理过程揭晓后,也许你会感觉非常简单;但刚读完题和看完图时,你的第一感觉很可能是——无从下手。
如果你仅仅根据和的关系去尝试填出这7个圆圈内的数,除非有中彩票大奖的运气,否则必定要经历很多次失败。而对大多数人来说,四五次失败就足以把他们打击到放弃努力了。
事实上,这个题目并没有要求确定每个圆圈内的数,而只要求确定其中一个特定位置上的数。这道题的设计,是希望引导孩子从单个的和关系的推导提升到整体的和关系的分析——前者是我们通常能“自然而然”地想到的办法,而后者则需要通过系统性的训练才能建立起来。再多延伸说一句,“全局性推理”是数学方法论中一个重要且普遍应用的思维模式,不仅对于数学问题,而且对我们思考不同领域内的问题都大有裨益。
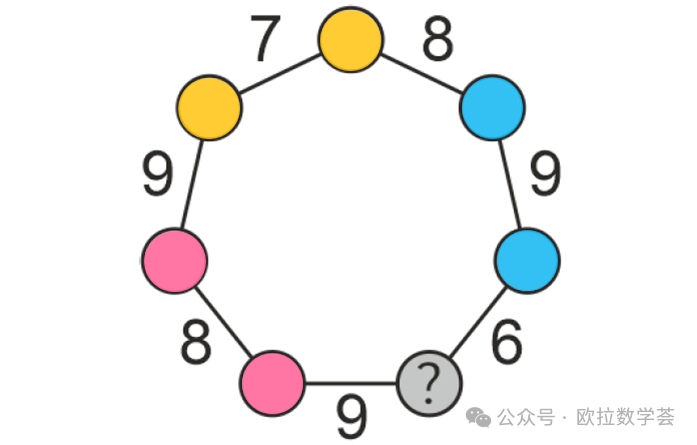
在上图中,我们同时考虑三个和关系。两个红色圆圈内的数之和是8,两个黄色圆圈内的数之和是7,两个蓝色圆圈内的数之和是9。所以三组共6个数的和是8+7+9=24。而从1到7这7个数的和是1+2+···+7=28。所以剩下的那个数应该是28-24=4,也是打问号的圆圈内必须要填的数。虽然这三组共6个数应该填的位置我们一个都没有确定,但我们可以肯定(如果要满足题目的条件)它们的和一定是24,进而推断打问号的圆圈内必须填4。
尽管上面的做法只是填出了一个特定圆圈内的数,但从这个数出发,我们就能把其他圆圈内的数逐个填出来。
一般地说,只要能确定其中任意一个圆圈内的数,就能把所有圆圈内的数都填出来。这里我再多提一个问题:如果我们要求先确定正上方的圆圈(即和数7右边的黄色圆圈)内的数,你有没有什么巧妙的办法?LEVEL C
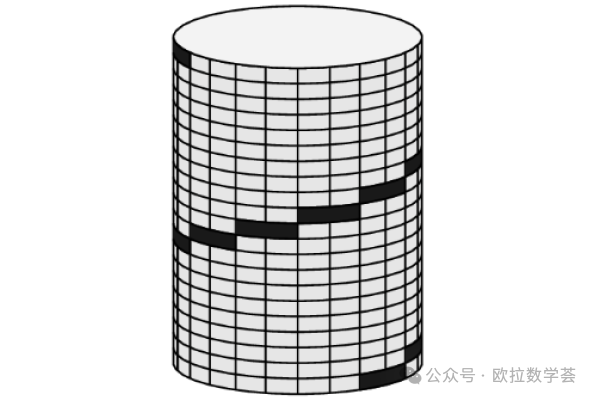
1. 如下图所示,圆柱形塔有一个梯子从底部直通到顶部。梯子的每个梯级都一样高。图中可以看到9个梯级。还有多少个梯级是看不见的?(3分题)
2. 一个露台上铺着三种不同大小的正方形瓷砖。最小的瓷砖周长为80厘米。如图所示,一条蛇沿着瓷砖的边缘躺在露台上。这条蛇的长度是多少厘米?(4分题)
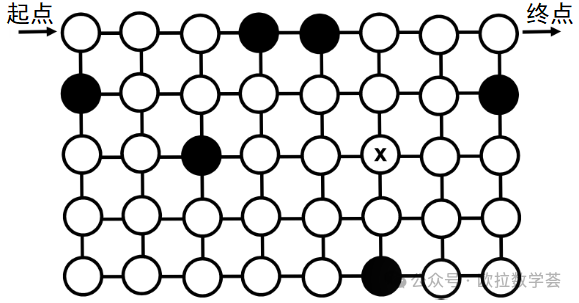
3. 莫妮卡想在迷宫里找到一条从左上方的圆圈开始,到右上方的圆圈结束的路径。她只能水平或垂直移动到相邻的圆圈,并且只能移动到白色圆圈。此外,每个白色圆圈都要恰好经过一次。当她到达标有X的圆圈时,下一步是向哪个方向移动?(5分题)
解答和点评
第1题是图形观察题。通过观察梯子,可以发现塔身的每一行都刚好有一个梯级。所以梯级的总数就是塔身的行数。直接数出塔身共有21行(建议至少数两遍,以确保没有数错),所以有21-9=12个梯级是看不见的。
第2题是图形计算题。根据三种正方形瓷砖的摆放关系,可以推出从小到大的边长分别是20,40,60厘米(具体推导过程不在这里赘述)。把蛇身分成12段,然后再把各段长度相加,可得蛇的长度是20×5+40×5+60×2=420厘米。
第3题的图的设计非常巧妙,用“独具匠心”来形容也不为过。满足题目要求的路径事实上只有一条,而为了确定这条路径,我们需要从起点开始一步一步地、像扫雷一样确定下一步应该到达哪个圆圈的位置。要在限时的考试中通过准确的推理把这条路径找出来,对孩子的分析能力是很大的挑战。不过,我并不认为这道题的意义仅仅是训练我们在短时间内(例如5分钟)完成整个推导过程。如果你能用20或30分钟完成,这仍然是非常有益的训练过程。完成时间的长短固然反映了能力的高低,但无论时间多长,训练的作用都是一样的。
每个LEVEL的5分题都是难度最高的题目。从这三道5分题的解答中,我们也可以观察到孩子的分析和推理能力的构建是怎样逐步展开和推进的。