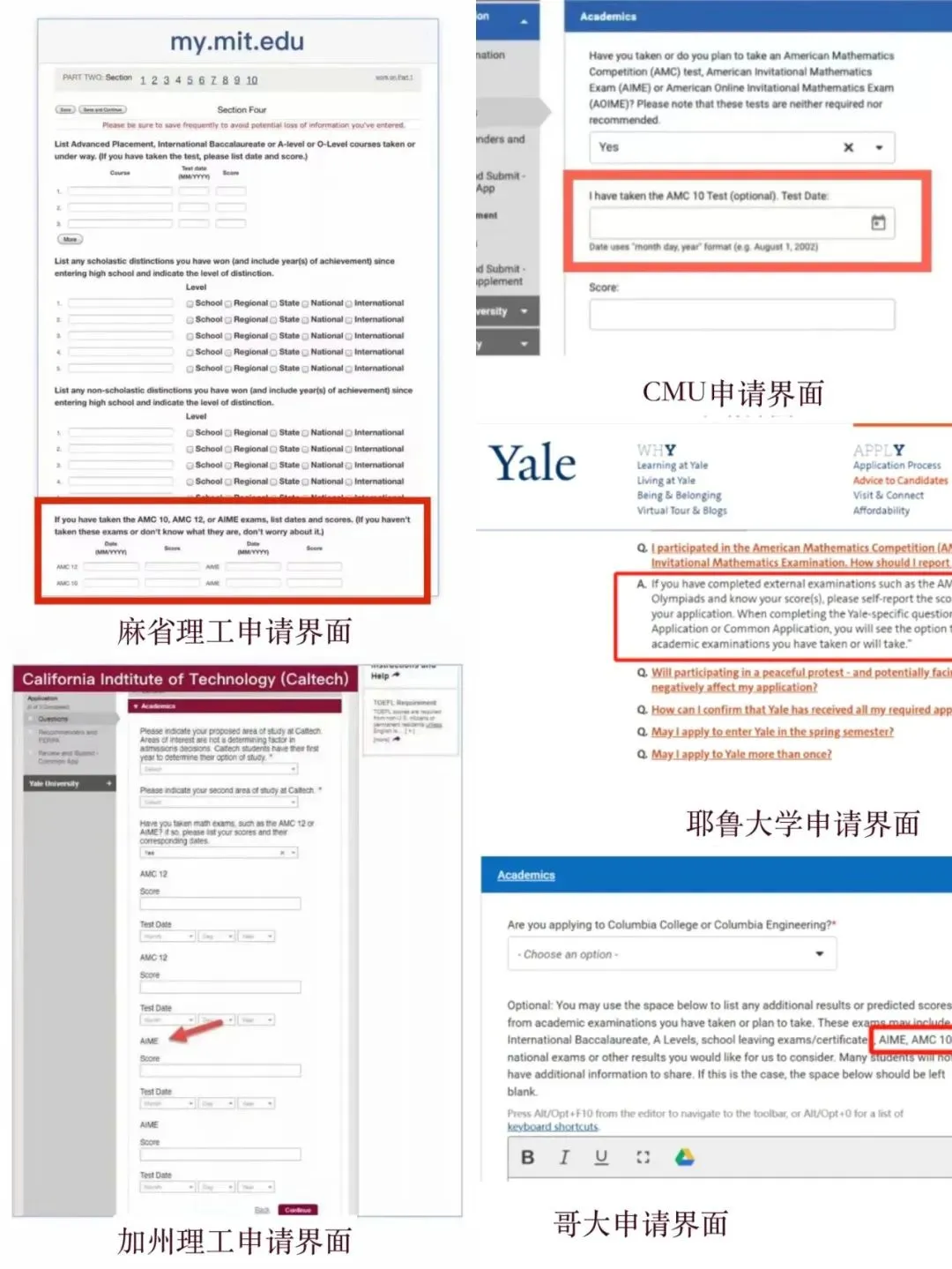
2025 SUMaC数学夏校申请通道已开启!
2025年SUMaC计划招收104名学员,其中线上64人,线下40人,
名额有限,竞争激烈!
近年来,顶尖大学的招生官员开始将夏校看作是一种选拔杰出学生的“利器”。
今年,芝加哥大学针对参加过芝加哥大学夏校(Pre-College Summer Session)的学生开放一条新的早申请通道:Summer Student Early Notification(夏校学生提前轮,简称SSEN),申请提交后三周即可获得录取结果。
芝大这次的“ED0”举措让夏校从一个申请“点缀者”的位置上升到“重大影响者”甚至“决定者”的位置,给申请者多了一次申请机会。这也让众多有意留学的家庭深刻认识到参加名校举办的夏校的重要性。
ROSS、PROMYS、SUMaC在数学夏校内名声极大,并称三大美国数学训练营。目前,SUMaC夏校已开放申请,这么高含金量的夏校,数学er不容错过!
斯坦福大学数学夏令营SUMaC
斯坦福大学数学夏令营(SUMaC)开始于1994年,由美国数学协会Epsilon基金和斯坦福数学系共同资助,是一个针对高中生数学能力拓展的学术型项目。

从项目开始1995年招收了第一批共12名学生,此后很长一段时间,SUMaC为了保证参与项目的学生都能得到足够多的关注和收获,严格限制每届40人的招生规模。
疫情期间,Sumac线下营的活动调整为线上举行。而自2022年起,Sumac线下营恢复但同时保留线上营(人数与线下营基本相当),算是历史性地第一次扩营,对于众多希望申请这个高质量夏校的优秀的学生来说是很大的利好。
官网地址:https://sumac.spcs.stanford.edu/
申请时间
已开放申请
申请截止时间:2025年2月3日(太平洋时间)
录取通知时间:2025年4月中旬
面向学生
10-11年级学生
对数学感兴趣,有较强的高中几何和代数掌握能力。
线下项目(Residential Program)招收40人
线上项目(Online Program)招收64人
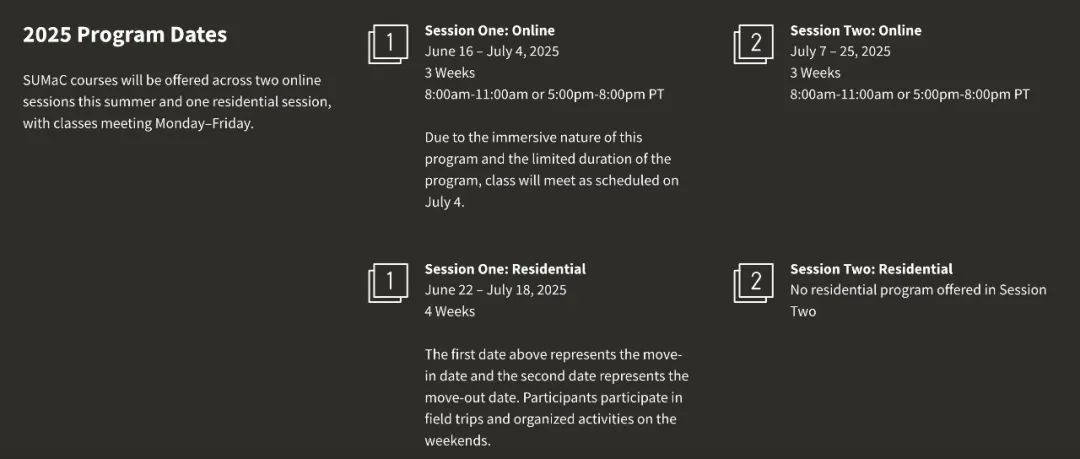
时间安排
SUMaC 课程将于今年夏季以两个线上课程和一个线下课程的形式提供,上课时间为周一至周五。
线下项目:2025 年 6 月 22 日至 7 月 18 日
线上项目:
Session1:2025 年 6 月 16 日至 7 月 4 日
Session2:2025 年 7 月 7 日至 25 日
申请材料
✅申请表(含数学测试题)-Online Application Form
✅学术证明-Academic Records
✅老师推荐信-Teacher Recommendation
✅额外材料(可选)-Optional Video Essay
✅$65申请费
✅对入营测试题的解答
出勤政策
线上:参与者必须全程参与课程,并应远程出席所有课程和活动。参与者必须在指定的每日上课时间参加课程,并打开麦克风和摄像头。
所有活动旨在为参与者提供课堂内外的全面体验。参与者不应承担任何与必修课程活动直接冲突的非课程承诺。
线下:参与者必须全程参与课程,并应出席所有课程活动。学生必须在指定的抵达日期抵达并留到课程结束。
所有活动(包括课外活动)都旨在为参与者提供课堂内外的全面体验。参与者只能因健康原因、宗教信仰或家庭紧急情况而缺席预定的活动。
SUMaC数学营学术方向
SUMaC提供两门课程,分为Program I和Program II。每个学生参加两门课程中的一门。学生可以在申请中表明他们在两种课程选项之间的偏好,然后招生委员会将录取的学生招入他们的最终课程。这两门课程都以数学的核心主题为基础,强调其历史意义和与当前数学研究方向的相关性。
Program I:抽象代数与数论
主题:通过五个有启发性的问题介绍,如尺规作图、二维图案的分类、纠错码、密码学和结构对称性分析。
申请Program I 的学生应该有书写和阅读数学证明的经验,以及扎实的几何和代数掌握能力。
▶ Program I申请者应该能够熟悉:
• 通过归纳、矛盾、反证等方式证明命题。
• 各种数学逻辑,例如基本的逻辑符号及其含义,如 if、then、or等。
• 集合相关的表示。
被Program I录取的学生通常学习过数论,熟悉模数运算和一些涉及模数运算的基本理论结果。无需参加过数学竟赛或比赛。
Program II:代数拓扑
Program II以代数拓扑学为中心,这是当前数学研究的一个主要领域。
拓扑学是研究不受变形影响的形状的性质(拓扑性质)。例如,由橡胶制成的球体可以变形为立方体的形状。虽然看起来球体和立方体没有太多共同点,但事实证明它们在拓扑上是等价的,并且可以在数学上精确化。本课程将探讨使用代数概念(例如群的概念)分析形状拓扑性质的不同方法。
▶ Program II的申请人应具备:
• 比Program I学生有更多的进行数学证明的经验。
• 对高等数学有浓厚的兴趣。
• 有抽象代数如群论的学习基础,但不是必需的。
注意:Program II 的学生通常是Program I 的先前参与者,或者对Program I的内容有经验。
2025年测试题