写这篇每月一题的时候正好Bosniaand Herzegovina的IMO TST题目出来了,以前做题目的时候总是想看看小国家是怎么备考IMO的,并且他们的TST难度似乎也很适合USAMO的考试。
因此本月的每月一题给出今年Bosniaand Herzegovina第二天的第三题:
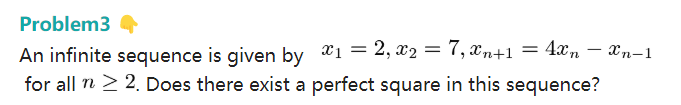
Sketch:
本题如果换成问一下这个数列中平方数的个数的话,可以直接作为一个AMC12的中段题目来考,可惜他现在是个TST当中的证明题。自己写几项之后就可以得到一个否定的答案,问题在于如何证明。
首先应当使用特征方程或者生成函数得到这个数列的通项公式,特征方程方法在往期的每月一讲中已经出现过,这期就给一个生成函数的做法:

有了这个通项公式的结果,我们只需要估计第几项有可能是平方数。常用的套路是寻找合适的模,这里我们选择模5.
由于任何整值线性递推数列的模数列都是周期的,我们可以得到这个数列的模数列:2,2,1,2,2,1,2,2,1,...

最后:
这个题目在波黑TST中原题是设X1=1,从而他们的国家队宣布本题不予评分。











