今天我们给出第六组袋鼠竞赛的题目(每个年级组一道题),并附上解答。
1-2年级组
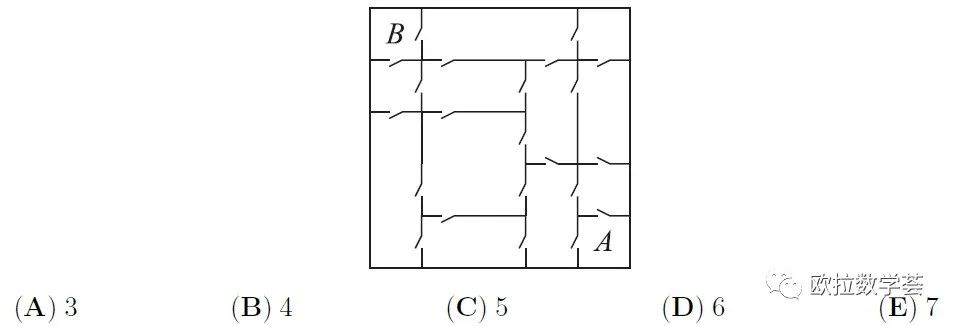
In Baby Roo's house, each room is connected to any neighboring room by a door as shown in the picture. Baby Roo wants to get from the room A to the room B. What is the least number of doors that he will need to go through?
在Baby Roo的房子里,每个房间和与它相邻的房间之间都有一扇门相连,如下图。Baby Roo想从房间A走到房间B。他最少需要经过多少扇门?
3-4年级组
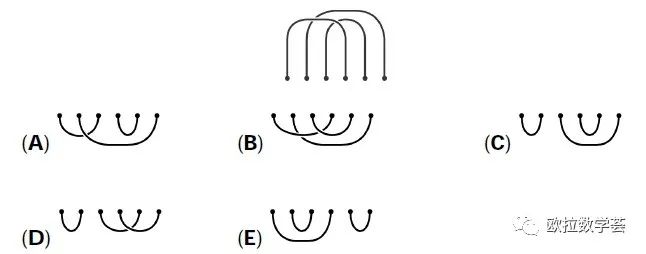
Three ropes are laid down on the floor as shown. You can make one big, complete loop with three other pieces of rope. Which of the ropes shown will give you one big loop?
三条绳子如下图那样放置在地板上。你可以利用另外三条绳子,与这三条绳子一起构成一个大的绳圈。你可以用下面哪组绳子做到?
5-6年级组
A train has 12 coaches. Each coach has the same number of compartments. Mike is travelling in the third coach and in the 18th compartment from the engine. Jane sat in the 7th coach in the 50th compartment from the engine. How many compartments are there in each coach?
一列火车有12节车厢,每节车厢里有相同数量的隔间。Mike位于第三节车厢,坐在从火车头数过来的第18个隔间。Jane位于第七节车厢,坐在从火车头数过来的第50个隔间。每节车厢里有多少个隔间?
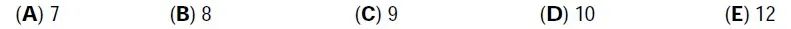
7-8年级组
Two pieces of rope have lengths 1 m and 2 m. Alex cuts the pieces into several parts. All the parts have equal lengths. Which of the following could not be the total number of parts he obtains?
两条绳子的长度分别为1米和2米。Alex把它们剪成小段,每段绳子都一样长。下面哪个数不可能是他得到的绳子的段数?
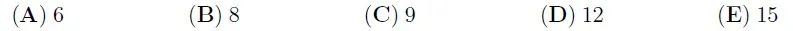
-------- 分割线 --------
下面是第六组题目的参考答案和解析。
1-2年级组
In Baby Roo's house, each room is connected to any neighboring room by a door as shown in the picture. Baby Roo wants to get from the room A to the room B. What is the least number of doors that he will need to go through?
在Baby Roo的房子里,每个房间和与它相邻的房间之间都有一扇门相连,如下图。Baby Roo想从房间A走到房间B。他最少需要经过多少扇门?
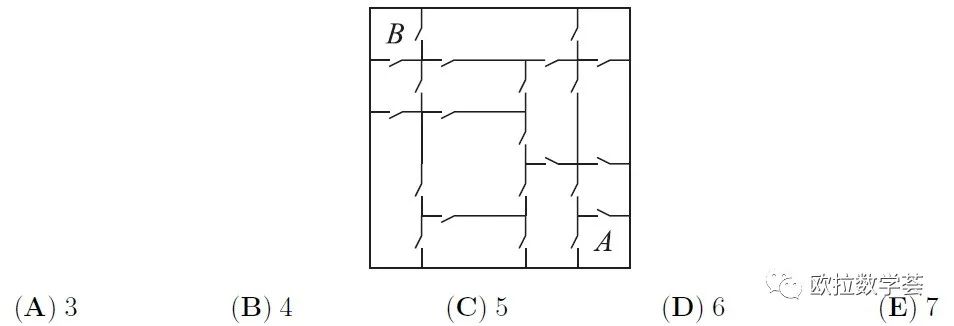
【答案:B】这是一道考验观察力的题目。要找到一条需要通过5扇门的路径是比较容易的。但确实存在只需通过4扇门的路径。如下图。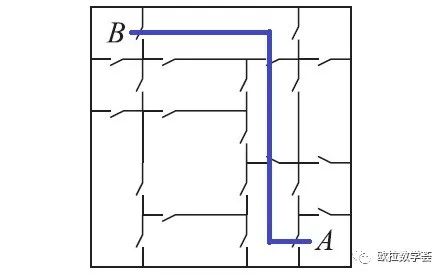
3-4年级组
Three ropes are laid down on the floor as shown. You can make one big, complete loop with three other pieces of rope. Which of the ropes shown will give you one big loop?
三条绳子如下图那样放置在地板上。你可以利用另外三条绳子,与这三条绳子一起构成一个大的绳圈。你可以用下面哪组绳子做到?
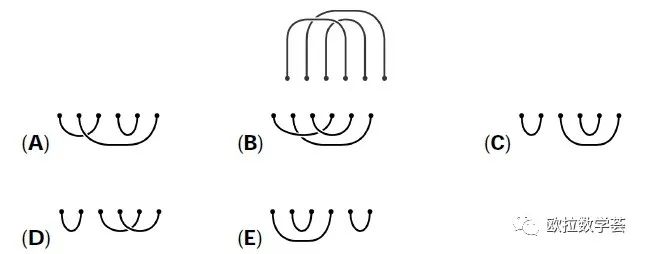
【答案:C】如果直接对每个选项进行验证,很容易看得眼花。更好的策略是利用一个结论:如果要构成一个大的绳圈,就不能形成小的绳圈。具体来说,选项中的任意一条绳子,不能与原来的三条绳子中的一条构成一个绳圈。 从左到右把6个接点编号为1~6,则接点1和4属于同一根绳子,接点2和6属于同一根绳子,接点3和5也属于同一根绳子。选项(A)中,接点2和6来自同一根绳子;选项(B)中,1和4来自同一根绳子;选项(D)中,3和5来自同一根绳子;选项(E)中,1和4来自同一根绳子。所以,这四个选项都会形成小的绳圈,从而不可能构成一个大的绳圈。
需要特别注意的是,如果绳子的数量超过3根,则第一段中的结论不成立。比如4条绳子,有可能是形成两个小的绳圈,每个绳圈都由4根绳子(2根是原来的绳子,2根是选项中的绳子)构成。
5-6年级组
A train has 12 coaches. Each coach has the same number of compartments. Mike is travelling in the third coach and in the 18th compartment from the engine. Jane sat in the 7th coach in the 50th compartment from the engine. How many compartments are there in each coach?
一列火车有12节车厢,每节车厢里有相同数量的隔间。Mike位于第三节车厢,坐在从火车头数过来的第18个隔间。Jane位于第七节车厢,坐在从火车头数过来的第50个隔间。每节车厢里有多少个隔间?
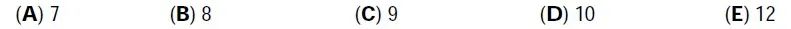
【答案:B】根据Jane的隔间编号,可知每节车厢应该有8个隔间。如果每节车厢的隔间数少于8,第50个隔间应该出现在第7节车厢之后(7×7=49);如果每节车厢的隔间数大于8,第50个隔间应该出现在第7节车厢之前(6×9=54)。
7-8年级组
Two pieces of rope have lengths 1 m and 2 m. Alex cuts the pieces into several parts. All the parts have equal lengths. Which of the following could not be the total number of parts he obtains?
两条绳子的长度分别为1米和2米。Alex把它们剪成小段,每段绳子都一样长。下面哪个数不可能是他得到的绳子的段数?
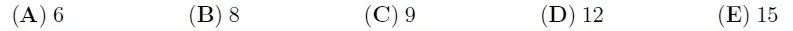
【答案:B】由于每段绳子都一样长,所以第二根绳子剪出的段数应该是第一根绳子的2倍。从而,所有绳子的数量应该是3的倍数。所有选项中,只有(B)的数不是3的倍数。