Math Kangaroo袋鼠数学竞赛真题解答（七）

今天我们给出第七组袋鼠竞赛的题目（每个年级组一道题），并附上解答。

1-2年级组

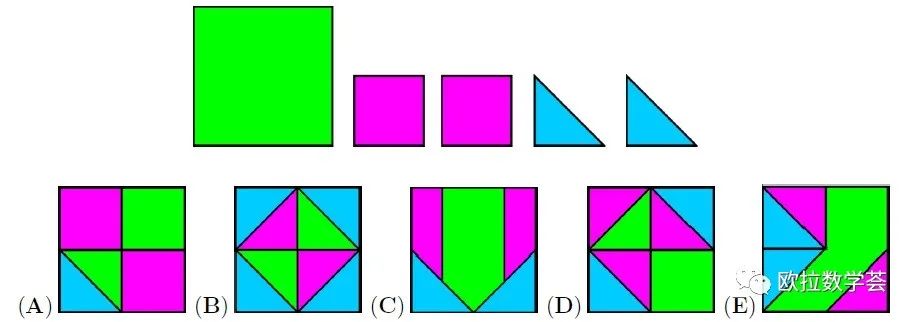
Which pattern can we make using all five cards given below?

使用所给的5张卡片，可以摆出哪个选项中的图案？

3-4年级组

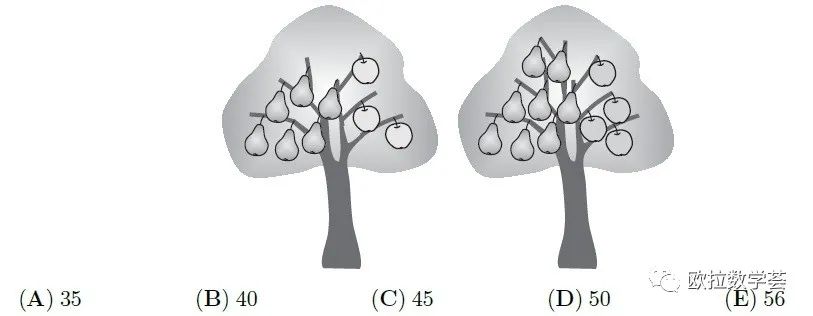
Magic trees grow in a magic garden. Each tree contains either 6 pears and 3 apples or 8 pears and 4 apples. There are 25 apples in the garden. How many pears are there in the garden?

魔术花园里种了一些魔法树。每棵树上要么结6个梨子和3个苹果，要么结8个梨子和4个苹果。已知花园里共有25个苹果，那么花园里共有多少个梨子？

5-6年级组

The number 2581953764 is written on a strip of paper. John cuts the strip 2 times and gets 3 numbers. Then he adds these 3 numbers. Which is the smallest possible sum he can get?

一张纸条上写了一个数2581953764。John把纸条剪了两刀，剪成3截。他把三截纸条上的三个数相加，所得的和数最小可能是多少？

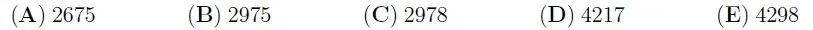
7-8年级组

Ivor writes down the results of the quarter-finals, the semi-finals and the final of a knock-out tournament. The results are (not necessarily in this order): Bart beat Antony, Carl beat Damien, Glen beat Henry, Glen beat Carl, Carl beat Bart, Ed beat Fred and Glen beat Ed. Which pair played in the final?

Ivor记录了一场淘汰赛的四分之一决赛、半决赛和决赛的结果。他记录的结果如下（不一定按照比赛顺序）：Bart战胜Antony，Carl战胜Damien，Glen战胜Henry，Glen战胜Carl，Carl战胜Bart，Ed战胜Fred，Glen战胜Ed。请问，哪两个人在决赛中对阵？

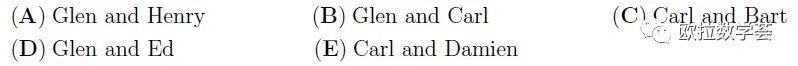
--------   分割线   --------

下面是第七组题目的参考答案和解析。

1-2年级组

Which pattern can we make using all five cards given below?

使用所给的5张卡片，可以摆出哪个选项中的图案？

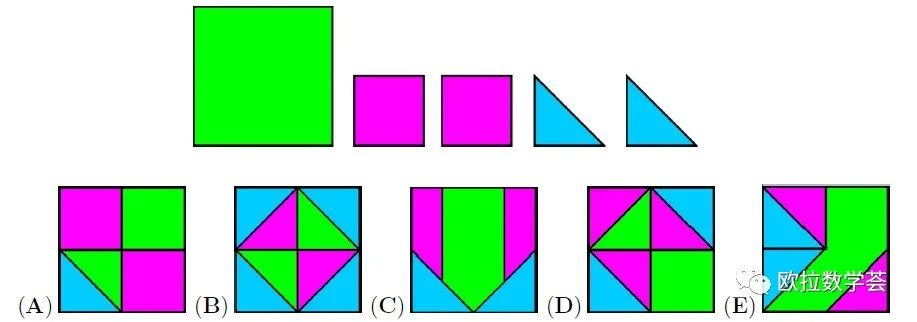
【答案：A】显然，卡片之间会有交叠遮盖的效果。选项（B）中，蓝色的面积比蓝色卡片的总面积大，所以不可能。选项（C）中，粉色部分不可能由两张粉色卡片拼出来。选项（D）类似于（C）的理由。选项（E）中，右下角的粉色区域不可能构造出来。

3-4年级组

Magic trees grow in a magic garden. Each tree contains either 6 pears and 3 apples or 8 pears and 4 apples. There are 25 apples in the garden. How many pears are there in the garden?

魔术花园里种了一些魔法树。每棵树上要么结6个梨子和3个苹果，要么结8个梨子和4个苹果。已知花园里共有25个苹果，那么花园里共有多少个梨子？

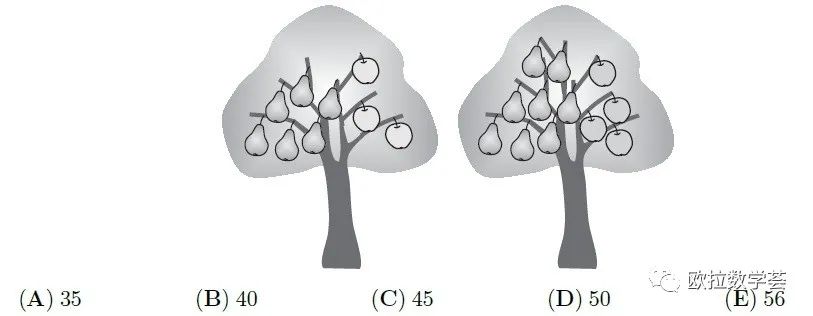
【答案：D】两种树的数量不确定，有多种可能性。但无论是哪种树，树上的梨子数量都是苹果数量的2倍。所以梨子的总数也一定是苹果的2倍。

5-6年级组

The number 2581953764 is written on a strip of paper. John cuts the strip 2 times and gets 3 numbers. Then he adds these 3 numbers. Which is the smallest possible sum he can get?

一张纸条上写了一个数2581953764。John把纸条剪了两刀，剪成3截。他把三截纸条上的三个数相加，所得的和数最小可能是多少？

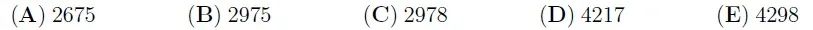
【答案：B】首先，要使和数的位数尽量少。因为三个数的总位数是10位，所以最大的加数至少是四位数。其次，要使四位数的加数的千位数字最小。所以首先应该考虑选择1953作为四位数的加数。此时，另外两个加数分别为258和764，三个数的和是2975。如果要使和数更小，四位数的加数千位数字不能大于2，对应的能得到最小和数的切分结果是（2581，953，764），它们的和显然大于2975。

7-8年级组

Ivor writes down the results of the quarter-finals, the semi-finals and the final of a knock-out tournament. The results are (not necessarily in this order): Bart beat Antony, Carl beat Damien, Glen beat Henry, Glen beat Carl, Carl beat Bart, Ed beat Fred and Glen beat Ed. Which pair played in the final?

Ivor记录了一场淘汰赛的四分之一决赛、半决赛和决赛的结果。他记录的结果如下（不一定按照比赛顺序）：Bart战胜Antony，Carl战胜Damien，Glen战胜Henry，Glen战胜Carl，Carl战胜Bart，Ed战胜Fred，Glen战胜Ed。请问，哪两个人在决赛中对阵？

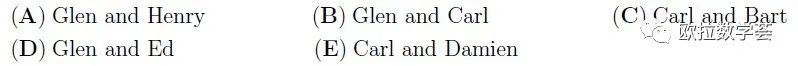
【答案：B】根据淘汰赛的规则，只要输一场比赛就不能继续参加后面的比赛了。所以，要打入决赛，必须在四分之一决赛和半决赛获胜。虽然题目中没有告诉我们哪些场次是什么类型的比赛，但我们可以统计获胜的场次。在所有7场比赛中，Glen获胜3次，Carl获胜2次，Bart和Ed获胜一次。所以应该是Glen和Carl进入决赛，并且是Glen获得冠军。