引言
现实生活中,我们常常会看到车祸的新闻(图 1),电影中也有不少车祸场景(图 2)。

图 1: 林志颖驾车撞上隔离带后车头起火
严重的车祸都伴随着猛烈的撞击和人员的伤亡。当车辆发生猛烈的撞击时,安全气囊和安全带就成了保护车内乘客的最后一道防线。

图 2: 电影《香草天空》中车辆坠桥的场景
如图 3 所示,安全气囊的工作原理是:当汽车受到一定的碰撞力时,气囊系统会引发类似小剂量炸药爆炸的化学反应,隐藏在车内的安全气囊会瞬间充气弹出,在人体撞击车内零部件之前被填充到位。

图 3: 安全带和安全气囊的重要性
当人体接触安全气囊时,气体会通过气囊表面的气孔排出,从而起到对人体的缓冲作用。根据美国高速公路安全管理局的调查[1],气囊的正确使用可令轿车的驾驶员死亡率减少11%,正面撞击时可降低 30% 的冲击力。

图 4: 汽车撞击中气球能代替安全气囊吗?
气球能代替安全气囊吗?就有这样一则流言:两个小丑带着一大堆气球去参加派对时出了事故,汽车以 56 km/h 的速度撞上了一堵墙。司机因系了安全带保住了性命,而坐在副驾驶上的小丑面前有一堆气球,在气球的缓冲下他也有惊无险地躲过了一劫(图 4)。这则流言是真的吗?接下来本文先简单介绍一下《流言终结者》的实验,然后再从模型角度来探究这个问题。
实验
针对“气球能否代替安全气囊”这个问题,美国科普电视节目《流言终结者》曾做过实验[2]。为了模拟汽车以 56 km/h 的速度撞击,节目组将汽车头朝下从 12.5 m 的高度坠落。每次坠落前,都会在主副驾驶座位上各放置一个假人,假人头部和胸部装有加速度传感器。实验表明,不系安全带的情况下,没有气球缓冲的假人胸部和头部承受的加速度峰值分别为 630 g 和 340 g(其中 g = 9.8 m/s² 表示重力加速度,下文同)。高速摄像机显示,车辆在撞击地面的瞬间,假人头部直接撞在了挡风玻璃上(图 5 左上)。



 图 5: 《流言终结者》车辆撞击实验
图 5: 《流言终结者》车辆撞击实验
如果在假人前塞满普通气球,假人胸部和头部承受的加速度峰值分别为 620 g 和 350 g(图 5 右上),这与没有气球时几乎没有区别。高速摄像机显示,车辆在撞击地面的瞬间,车内有些气球直接炸掉了。为此,节目组换上了更结实的大型厚乳胶气球,高速摄像机显示,汽车撞击地面的瞬间,假人的头从气球的缝隙里透了出来,然后又被气球弹了回去,似乎没有受到什么伤害(图 5 左下)。传感器数据显示,假人头部和胸部承受的加速度峰值分为 115 g 和 130 g,尽管相对于普通气球的情况已经下降了很多,但超过 100 g 的加速度仍然是致命的。此外,节目组还对更多类型的气球和不同的放置方式进行了实验(图 5 右下),但结果都没有比大型厚乳胶气球更好。
模型
上面的实验已经证实:气球并不能代替安全气囊。为什么不同类型的气球和放置方式都不能将乘客的加速度降低到 100 g 以下?接下来本文将从模型角度来探究这个问题。
缓冲距离
首先,本文估计一下车辆撞击过程中要保证乘客存活下来需要的最短缓冲距离。《流言终结者》节目组认为人体在极短时间内能承受的极限加速度为 a= 100 g = 980 m/s²。乘客想要在车祸中存活下来,其在车辆撞击过程中承受的加速度峰值必须小于这个极限值。
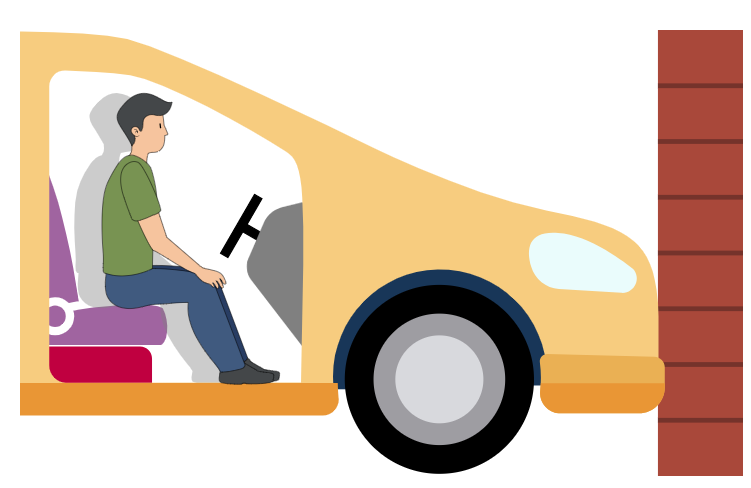
图 6: 车辆撞击后的缓冲距离
如果车祸过程中,身体以极限加速度从撞击前的速度υ0 降为 0,则需要的最短缓冲距离 Δχ 满足:
![]()
本文要研究的车祸中,车辆撞击前的速度为 υ0 = 56 km/h = 15.6 m/s。因此,要使乘客在撞击过程中存活下来,最短缓冲距离为:
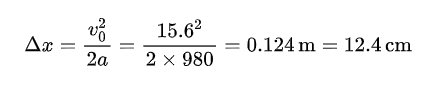
也就是说,车辆撞击后乘客至少需要继续减速运动 12.4 cm 才能活下来。这个距离并不算大,普通汽车是有足够的空间来让乘客减速的:坐在正副驾驶座位上的乘客,其头到挡风玻璃的距离约为 50 cm,腹部到仪表板的距离约为 30 cm。这实际上就是安全带和安全气囊的工作原理(图 3):安全带和安全气囊会施加适当的阻力来让乘客在撞到仪表板和挡风玻璃之前停下来,但又不会让乘客在太短的距离内停下来。
运动方程
通过上文对缓冲距离的计算,可以发现适当的机制(安全带、安全气囊)是完全可以以安全的加速度来将乘客停下来。理论上,气球有可能是这种适当的机制之一吗?接下来,本文来研究一下乘客头部在气球缓冲作用下的运动状态。
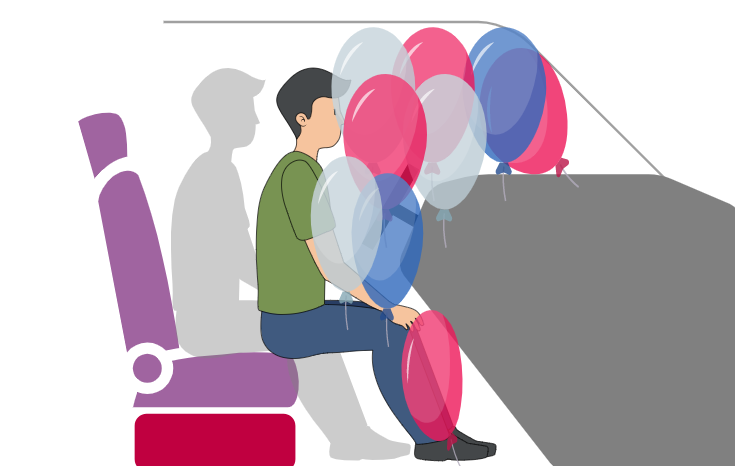
图 7: 车辆撞击后的气球压缩
为了简化问题,本文将气球内的气体看成是理想气体。由于车辆撞击的时间极短,气球在被压缩时,气体来不及与周围环境进行热交换。因此,可以将车辆撞击时气球内的气体压缩过程看成绝热过程,气体的体积 V 和压强 P 遵循以下关系:
![]()
其中 C 和 ϒ 为常数。对于常见的气球填充气体氦气(单原子气体),ϒ = 5/3。为了简化问题,本文将乘客头部前这一叠气球简化为圆柱(鸡都能假设为球形,这个假设不过分吧?),并且头部对气球的压缩仅发生在圆柱的轴向(图 8)。
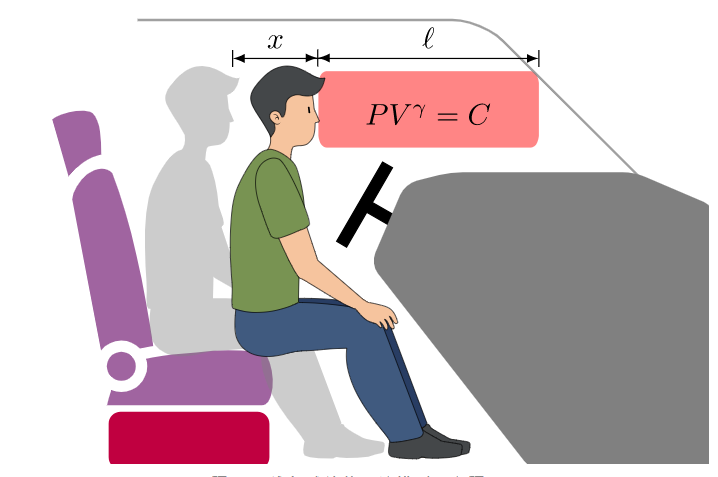
图 8: 一维气球绝热压缩模型示意图
用 x 表示头部压缩气球的长度,L0 表示气球被压缩前的长度,则被压缩后的气球长度可表示为 L0 = L0-x ,气球内气体的压强可以表示为:
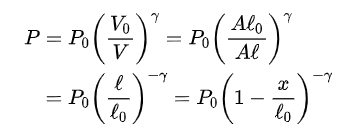
其中P0 和 V0为气球未被压缩时内部气体的压强和体积,A 为圆柱底面积(= 正脸面积)。上式表明气球对外界施加的力与L‾^5/3成正比,力随着气球的压缩急剧上升。图 9 给出了气球长度L 变化与气球压强P 的变化关系。从图中不难看出,L 每减少 1/3,气球对外界施加的力(或压强)几乎就翻倍。
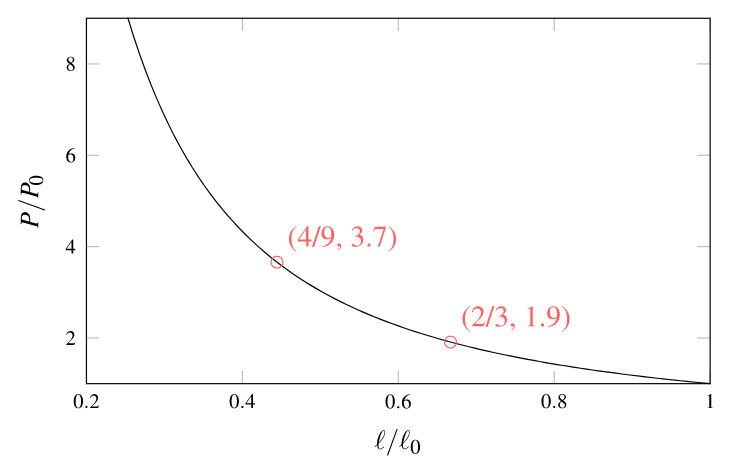
图 9: 气球长度比与压强比的关系
普通气球内的气压约为 820 mmHg(即 109 kPa)[3],比标准大气压 101 kPa 略高。这也很容易理解,气球并不能维持太大的压差。为简化计算,假设气球内的初始压强 P0 与外界环境一致,等于标准大气压。气球被压缩时对外界施加的力 PA,一部分用于抵消气球外的大气压力 P0A,剩余的力才是作用于乘客头部的力:
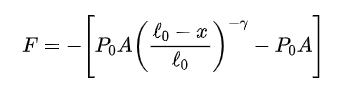
上式中右端的负号表示作用力的方向(与x 的正向相反)。因此,乘客头部的运动方程(加速度)为
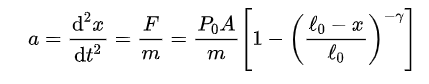
其中t 表示时间, m为乘客头部的质量。记乘客脸与气球刚接触时为时间零点(t = 0),则有以下初值条件:
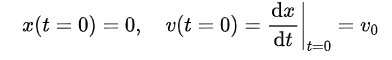
现在只需要给出参数的值,就可以数值求解乘客头部的运动方程。成年人头部质量一般占体重的 8.3% 左右[4],考虑一个体重 60 kg 的乘客,其头部重量m = 60*8.3%= 5 kg,正脸面积A = 300 cm²;考虑到乘客头部到前挡风玻璃的距离约为半米,假设模型中气球的长度L0 = 0.5 m;车辆撞击前的行驶速度为 u0= 15.6 m/s。将这些参数值代入以上两式,并由 MATLAB 函数ode45数值求解,结果如图 10 和 11 所示。
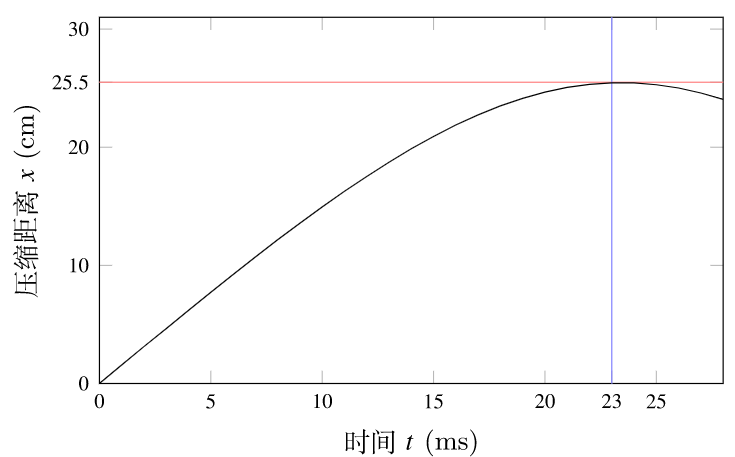
图 10: 压缩距离随时间的变化
结果显示:车辆发生碰撞后约 23 ms,气球被压缩距离达到了最大约 25.5 cm(图 10)。此时速度降为了 0,加速度达到了最大(峰值)约 149 g(图 11)。
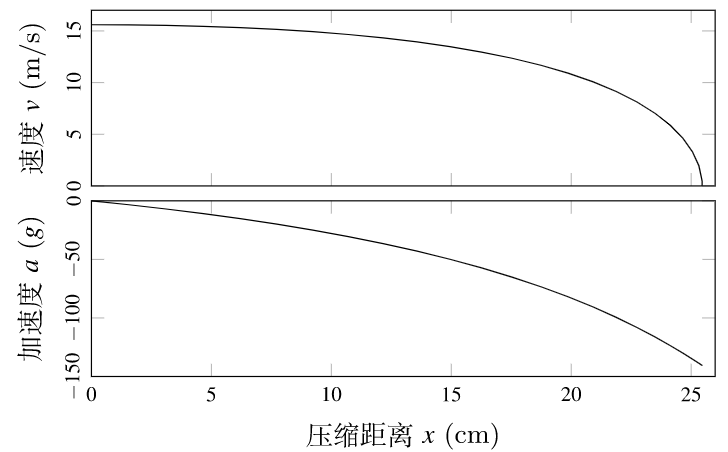
图 11: 速度和加速度与压缩距离的关系
结果表明,气球不能以 100 g 以内的加速度将乘客停下来,原因是气球被压缩时,内部压强急剧上升,还没能够使乘客停下来时,压力就已经增加到特别大,以至于使乘客头部的加速度超过了 100 g。实际上,对于普通的气球,在被压缩的早期就爆炸了,根本不会起到什么阻碍作用。上文的讨论中,实际上假设了气球在压缩过程中不会爆炸,这相当于《流言终结者》实验中使用的大型厚乳胶气球。
参数分析
上文中建立了乘客头部的运动方程,并在一定的参数下进行了求解。结果表明,气球不能以 100 g 以内的加速度将乘客停下来。现实生活中,不同乘客有着不同的头部质量 m 和正脸面积A ,不同型号的车辆有着不同的气球长度 L0(模型中用气球长度表征车内的空间)。如果适当地调整参数的取值,这个结论还成立吗?本节将分析各参数取值对加速度峰值的影响。
乘客头部运动方程的求解并不能直接给出加速度峰值。为了方便分析,接下来本文根据功能关系给出加速度峰值的直接求解方法[5]。加速度达到峰值时,实际上就是气球被压缩量达到最大时,假设此时气球长度为L1 。乘客头部将气球的长度从L0 压缩到 L1,需要做功为
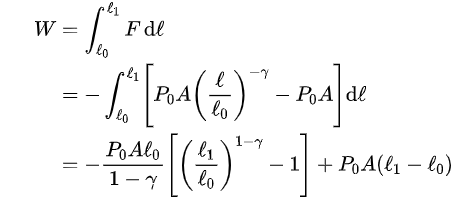
若乘客头部质量为 m,以初速度u0 压缩气球,则乘客头部动能全部用来压缩气球做功,即:

上式两端同时除以 P0AL0 可以整理成关于L1 /L0 的方程:
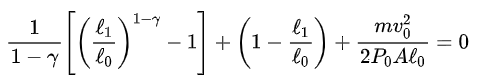
其中 0 < L1/L0 <1。如果上式中除了L1 以外的参数都已知,则由数值方法可以求得L1 /L0。由此,就可以根据以下公式求得乘客头部的加速度峰值大小:
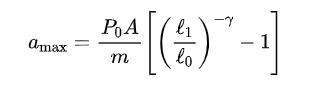
本文先用之前的参数取值计算一下加速度峰值,并与运动方程的求解结果对比:将头部重量 m= 5 kg,正脸面积A = 300 cm²,气球的长度 L0= 0.5 m,车辆撞击前的行驶速度为u0 = 15.6 m/s 代入以上两式,可以计算出L1 / L0= 0.4918,加速度峰值α max = 1372 m/s² = 140 g,这与运动方程求解出的结果一致。
为研究参数取值对结果的影响,本文对 m、A 和 L0分别单独进行改变,变化范围从减小 50% 到增加 50%,并计算出相应的加速度峰值。计算结果如图 12 所示。从图中不难看出:头部质量 m 越大,加速度峰值 α max 越小;正脸面积 A 越小,加速度峰值 α max 越小;气球长度L0 越大,加速度峰值 α max 越小。但这三个参数的改变并没有能够将加速度峰值降低到 100 g 以下。
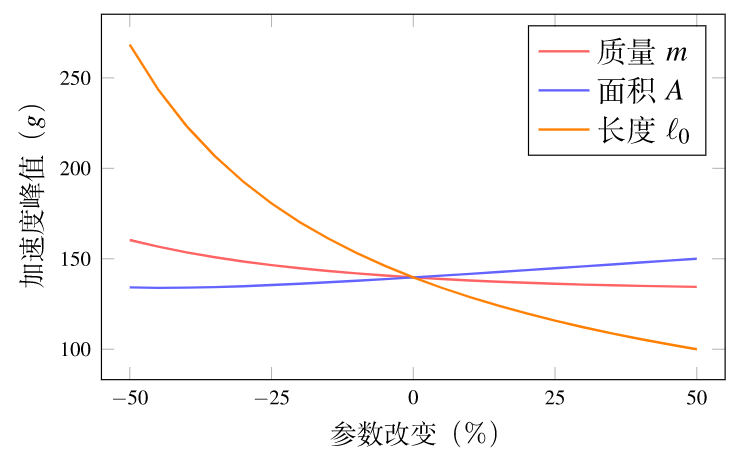
图 12: 参数灵敏度分析
考虑到气球内的氦气(单原子气体)可以更换为其它双原子气体(例如氮气),本文将 ϒ = 5/3(适用于单原子气体)更改为 ϒ = 7/5(适用于双原子气体),并重新计算了 m = 5 kg、A = 300 cm²、L0 = 0.5 m 和 u0 = 15.6 m/s 时的加速度峰值: α max = 1271 m/s = 130 g。
以上参数分析表明:单独改变m 、A、L0 和 ϒ,都不能使加速度峰值降低到 100 以下。但同时改变两个或更多参数是可以达到这一目标的:例如,当 ϒ = 7/5,L0 = 75 cm,其它参数不变时,α max = 92 g。
结论
本文针对“气球能否代替安全气囊”这个问题进行了建模分析。首先,本文计算了车辆撞击过程中乘客存活下来需要的最短缓冲距离。结果表明,正常车辆的内部空间是完全足够让乘客以安全的加速度停下来的。然后,本文将乘客压缩气球的过程简化为一维绝热压缩,根据绝热压缩的体积压强关系建立了乘客头部运动方程,并代入适当的参数对运动方程进行了数值求解。结果表明,气球无法以低于 100 g 的加速度将乘客停下来。最后,本文通过功能关系得到了加速度峰值,并研究了乘客头部质量、正脸面积、气球长度(车内空间)和气球内气体的类型对加速度峰值的影响。结果表明,单独改变这些参数确实会影响加速度的峰值大小,但都不能使加速度峰值降低到 100 g 以下。只有同时改变两个或更多的参数才有可能将加速度峰值降低到 100 g 以下。
模型的结果表明,通常情况下气球并不能代替安全气囊。普通气球在被压缩的早期就爆炸了,根本不会起到什么阻碍作用,而大型厚乳胶气球被压缩时,内部压强急剧上升,还没等乘客停下来,压力就已经大到使乘客头部的加速度超过了 100 g。与气球不同,安全气囊表面有大量气孔,当人体压缩安全气囊时,气囊内的气体会通过表面气孔排出,从而避免了压力的急剧上升。这就是气球与安全气囊的差别,也是气球不能代替安全气囊的原因。
参考资料
[1]Wikipedia contributors. Airbag — Wikipedia, the free encyclopedia, 2022: https://en.wikipedia.org/wiki/Airbag
[2]Mythbusters. Can balloons replace air bags in a car crash, 2012: https://www.youtube.com/watch?v=-0pjtFU_Cew
[3]jspchmst. Pressure of a latex balloon as it is inflated, 2008: https://www.youtube.com/watch?v=fwh-i0WB_bQ
[4]Robert Allison. Weight of human body parts as percentages of total body weight, 2012: https://robslink.com/SAS/democd79/body_part_weights.htm
[5]David Zaslavsky. Balloons as air bags: is there any hope?: https://www.ellipsix.net/blog/2012/10/balloons-as-air-bags-is-there-any-hope.html








