2019年第7届新加坡天文奥林匹克竞赛试题(二)
翻译:丛雨
封面图:三角座的发射星云Garren Nebula NGC604,图片来源:NASA
译者编译说明:
整场考试持续3.5小时,总分200分,题目具体分值使用了[]标注。
英文试题可在网站http://astronomy.sg获取,暂未找到常数表和答案解析。
题目翻译由个人完成,期间借助了谷歌翻译以及天文学名词数据库网站http://astrodict.china-vo.org,个人英文水平有限,部分题目的翻译质量欠佳。
数据分析题参考文献:
[1].Light curve data is derived from Tümer (1984) and downloaded from CALEB.
[2].Danjon A. Recherches de Photométrie Astronomique. Annales de l’Observatoire de Stras bourg. 1928;2: 1–185
[3].Evren S, Ertan AY, Tunca Z, Ibanoglu C, Kurutac M, Tümer O. Photoelectric photometry of Z Herculis.
[4].Astrophysics and Space Science. 1982 Oct;87(1-2): 51–9. Popper DM. Orbits of close binaries with CA II H and K in emission. I - Z Herculis and RS Canum Venaticorum. Astronomical Journal. 1988 Apr;95: 1242–50.
[5].Popper DM. Rediscussion of Eclipsing Binaries. I. Z Herculis. Astrophysical Journal. 1956 Jul;124: 196–207.
[6].Tümer O, Ibanoglu C, Tunca Z, Evren S. Light-curve analysis of Z Herculis. Astrophysics and Space Science. 1984 Sep;104(2): 225–44.
1.短问题 [12]
1.1 参宿七
1.2 伽利略卫星
1.3 消色差透镜
1.4 天鹰
1.5 毅力号
1.6 宇宙标度因子
2.中问题 [54]
2.1 太空填充
2.2 勒阿弗尔的日出
2.3 太空城
2.4 双子座流星群
2.5 引力测绘
2.6 星际质子
2.7 宇宙年龄
3.长问题 [34]
3.1 Part 1:恒星诞生
3.2 Part 2:恒星中年
3.3 Part 3:恒星死亡
4.数据分析:Seeing Double [40]
5. P(A) [10]
5.1 MCQ
5.2 MCQ
5.3 MCQ
5.4 MCQ
5.5 MCQ
6.P(B) [28]
6.1 辨别星座
6.2 冬季星空
6.3 夏季星空
7.P(C) [22]
7.1 Part 1
7.2 Part 2
7.3 Part 3
长问题部分[34]
在对恒星HD 85512的系外行星演化进行研究时,天文学家Tommy也许与其中一颗行星HD 85512b上的智慧生命取得了联系。这颗行星的质量大致为3.6 MÅ,轨道半长轴0.26AU,周期58.43d。为了进一步了解这个系外行星系统,Tommy收集了母星HD 85512的数据并和太阳对比:
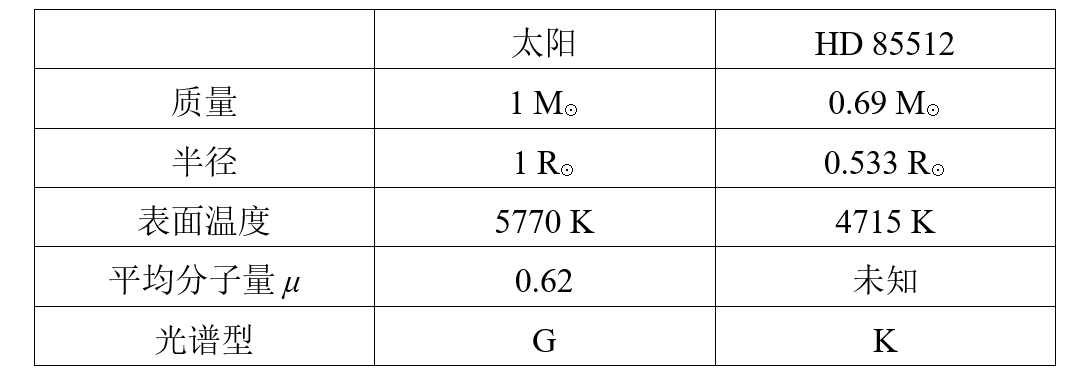
想要探究HD 85512的行星演化史,我们首先要对恒星的演化过程有一个较好的了解。在此问题中,我们要研究恒星的诞生、死亡以及平衡状态的热传递。
3.1 Part 1:恒星诞生(Star Birth)[9]
一般来讲,恒星形成于弥漫的分子云中。我们首先来探究分子云能够收缩并形成恒星的条件。
对于一个引力束缚系统,位力定理如下
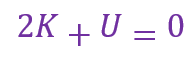
其中K和U分别是系统的动能和势能。
a).考虑密度均匀的球形分子云的情形,它的半径是R、质量是M。证明当其半径增加一厚度为Δr的球壳时,引力势能的变化量ΔU为
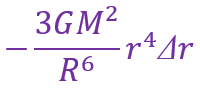
对上式积分可得到球形天体的引力势能
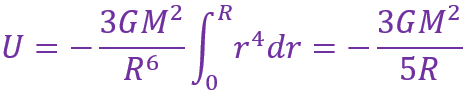
b).假设分子云是温度为T的理想气体,那么它的动能是(根据平均分子量为μ的分子随机热运动得出)
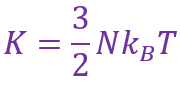
其中N是粒子数,kB是玻尔兹曼常数。给出球形分子云坍缩的最小半径和质量,将结果记作金斯长度RJ和金斯质量MJ。
这里只推断出了有关恒星HD 85512形成的少量信息,但我们还是对其有了一个粗略的了解。微小的扰动会触发分子云的引力坍缩,促进了恒星的形成。
3.2 Part 2:恒星中年(Star Mid-Life)[15]
分子云坍缩之后、主序星形成之前的阶段较为复杂,我们不做讨论。此部分题目的目标是研究恒星在流体静力学平衡状态下的热传递过程,特别是主序星。太阳和HD 85512都正处于主序阶段。
a).引力和压力梯度驱动着恒星的演化。将恒星视为对称的球体,且只考虑沿半径方向的作用力。对于密度为ρ(r)、横截面积为ΔA、厚度为Δr的微小质量![]() ,根据牛顿第二定律,证明它的运动方程为
,根据牛顿第二定律,证明它的运动方程为
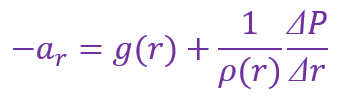
其中ar是径向的质量产生的加速度(向外为正方向)。并由此给出静力学平衡条件。
b).我们首先讨论对流的热传递。重力对其有重要的驱动作用,概述如下:
恒星内部的一团气体在上升时,会处于与它自身相比温度较低、密度较大的环境中,此时它会在浮力的作用下继续上升。气团下降时此理论同样适用。热量通过粒子的集体运动有效地传递。
在对流过程中,气体团的膨胀和收缩几乎是绝热的,因为气体团与周围环境之间没有足够的时间进行热传导。对绝热过程的描述如下:
当系统和外界没有热量交换时,发生的是绝热过程。此过程中理想气体的压力和密度ργ成正比,其中γ是绝热指数。
假设恒星由理想气体组成,证明对流的临界温度梯度为
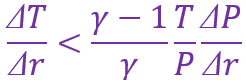
为了满足流体静力学平衡,压力梯度由下式给出
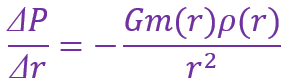
据此写出恒星达到流体静力学平衡时,对流的临界温度梯度的表达式。
c).接下来我们研究辐射的能量传输。我们要为辐射的温度梯度找到一个近似的表达式。
用L(r)表示恒星内部半径为r处的球表面的光度,即单位时间向外通过这一球面的能量。恒星中心的热核反应释放的能量导致L(r)随r增加,直到没有能量产生的区域为止。用ε(r)表示半径r处单位体积的产能率,那么显然有
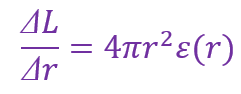
在中心核反应区之外,L(r)成为一个常数,接近恒星的表面光度。这一向外辐射的总功率L(r)与流量密度J(r)有关
![]()
而热辐射的流量密度J(r)等于
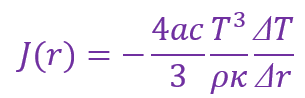
请由此给出辐射与对流的临界温度梯度相等时的条件。
d).恒星HD 85512核心处的数据大致是P= 1.7×1016Pa,T=13.7×106K,κ=0.138m2kg–1。计算对流占主导作用时单位质量的最小产能率。已知实际产能率是1.35×10–3W kg–1,评估你的计算结果。
e).不使用斯特藩–玻尔兹曼定律,估算HD 85512每秒辐射的单色光子数。
f).如果使用斯特藩–玻尔兹曼定律计算HD 85512的光度,那么每秒辐射的单色光子数会是多少?
3.3 Part 3:恒星死亡(Star Death)[10]
HD 85512在主序阶段之后,会像太阳一样演化成白矮星。
a).经典力学下白矮星电子的总能量如下给出
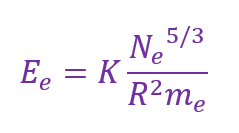
其中K = 1.23×10–68 kg3 m4 s–2,R是白矮星半径,Ne是电子总数,me是电子质量。
给出HD 85512到达白矮星阶段后的平衡半径的数值估计。
提示a):你也许会用到如下微分式:
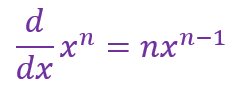
其中n是实数,x是变量。
b).假设电子的分布是均匀的,估算电子的速度,以光速c作单位。
提示b):电子之间的距离很近,我们可以采用德布罗意假说,即电子间距是德布罗意波长的两倍,德布罗意波长公式如下
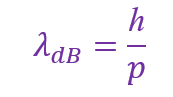
式中λdB是德布罗意波长,h是普朗克常数,p是粒子的动量。
c).考虑相对论效应的修正,电子能量如下
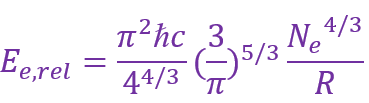
采用与之前类似的分析方式,估算HD 85512的临界质量Mc,以M⊙为单位。
需注意,如果白矮星的质量大于Mc,它将将发生坍缩。检查Mc是否依赖于恒星HD 85512自身的各项参数。此外,由于此问题使用了许多近似的计算,因此你的答案可能与著名的钱德拉塞卡极限有所不同。正确严格的推导超出了奥赛的大纲范围。
综上所述,此问题到此结束。看来Tommy必须更加努力才能理解HD 85512的系外行星系统。
数据分析部分[40]
4 数据分析:Seeing Double [40]
武仙座Z是一颗7等的食双星。你设置了光电探测器来检测它在B波段和V波段的视亮度变化,期间你记录了一系列较深的主极小和较浅的次级小数据。下表列出了V波段极小值的时间和星等: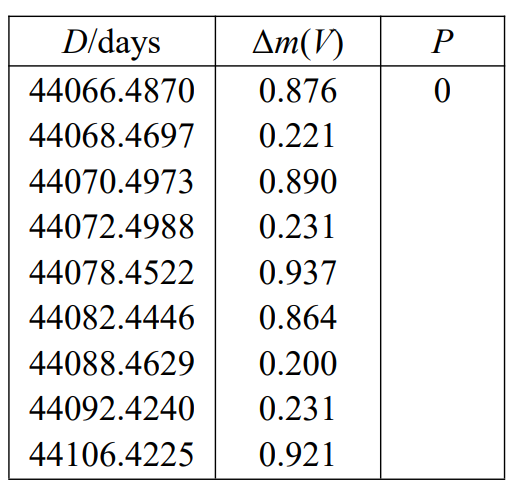
a).上面的表格并不完整,P代表了从D = 44066.4870天的第一次主极小开始经过的周期数。为每组数据填上合适的数值来补全这一列。
b).使用表中的数据绘制一幅合适的图像,以确定武仙座Z的星等变化周期T。保留3位有效数字。
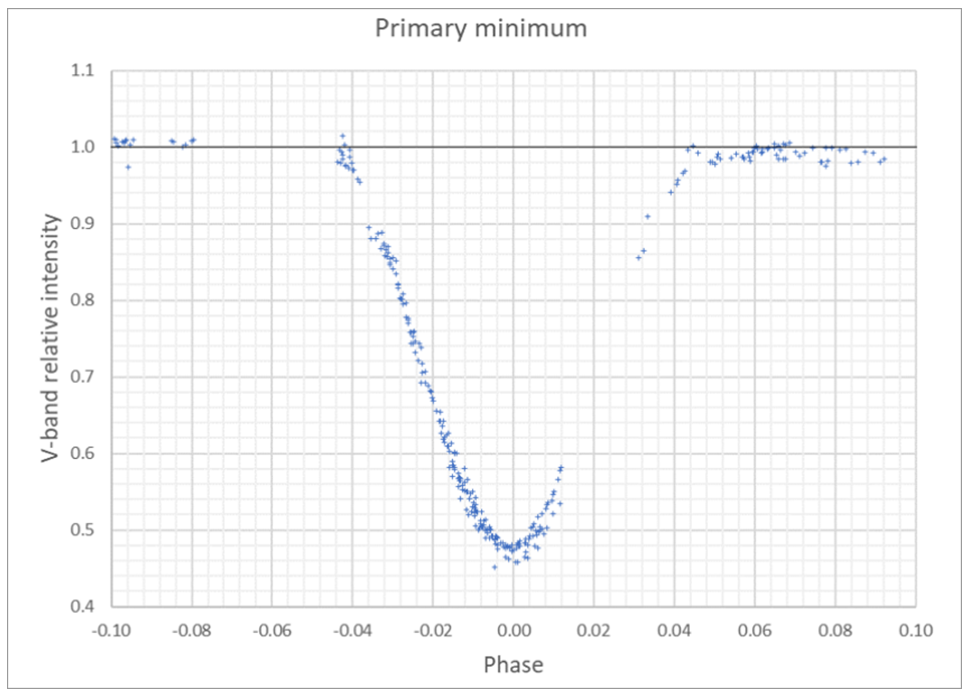
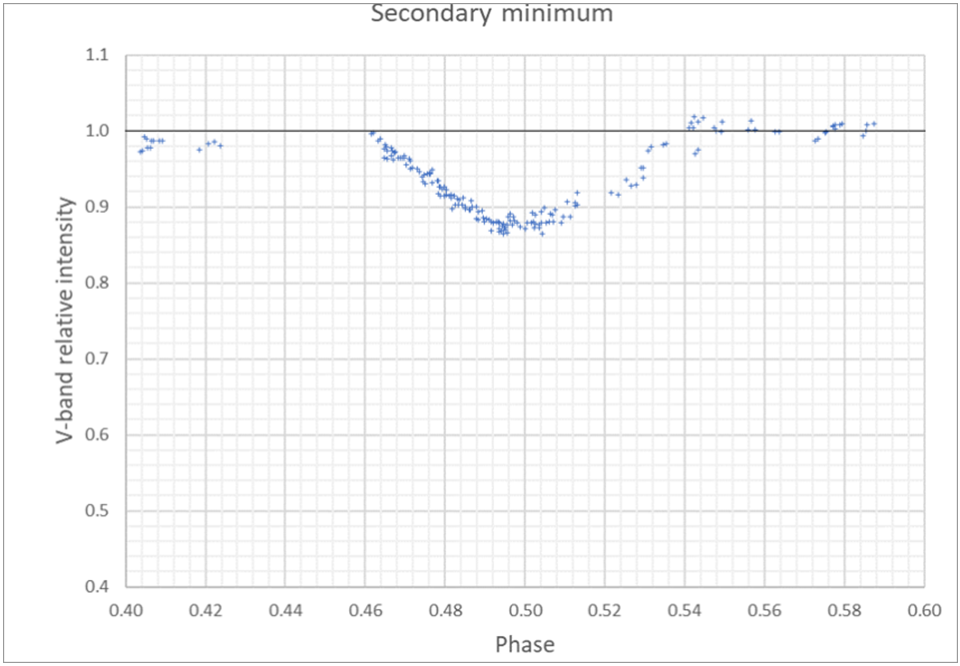
通过估测周期,我们可以重制武仙座Z的光变曲线,如以下两图,展示了主极小和次极小附近的数据,绘制了V波段的相对强度和相位(与轨道周期的比值)的关系。
c).根据光变曲线大致写出以下数值:
•τ1,主极小的持续时间,以相位表示
•τ2,次极小的持续时间,以相位表示
•I1,主极小的光强度
•I2,次极小的光强度
d).考虑食双星系统有一小一大两颗恒星,它们的半径比值k≤1,较小的恒星被较大的恒星遮掩而不可见的面积比例α0≤1。当大恒星掩小恒星、或小恒星凌大恒星时,亮度降低的比例分别为∆ioc和∆itr。假设恒星的亮度沿盘面均匀分布,证明
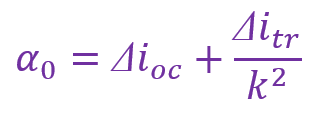
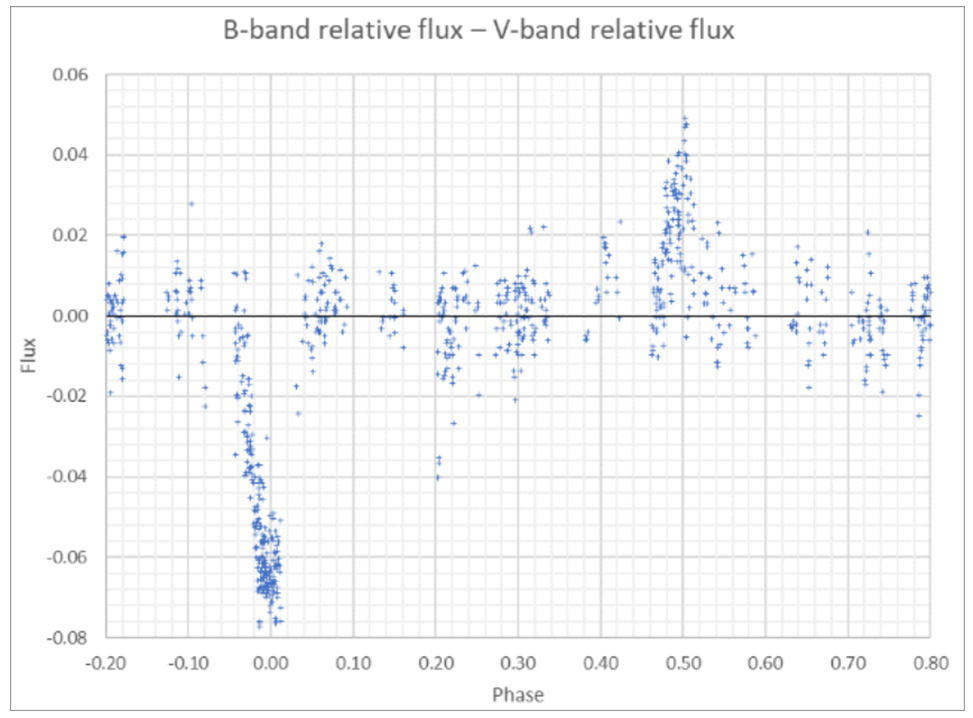
e).我们还根据观测数据绘制了武仙座Z的B波段和V波段的相对强度之差与相位的关系图。分析此图回答有关主极小的以下问题:
•这是一次掩星还是凌星?
•被食恒星的温度更高还是更低?
f).假如双星的轨道是圆形且轨道平面侧对地球(倾角等于0°),会发生α0=1的全食,且恒星的亮度仍沿盘面均匀分布。由此出发,在武仙座Z的主极小事件中被食的恒星记为A,使用目前已获取的信息算出下列数值:
•ρA,恒星A的半径与两星距离之比
•ρB,恒星B的半径与两星距离之比