接着上篇文章,2021年CMO的第二天的第二题——即第5题也是一个几何题。是一个尺规作图问题,题目如下:
 这个题目初看很简单,如果不要求步数,√2021一定能尺规作图作出来,因为我们可以尺规作出边长为1的等腰直角三角形,其斜边为√2,再以√2和1为直角边作直角三角形,则其斜边为√3,...依此类推,以√n和1为直角边做出直角三角形,则其斜边即为√(n+1),
这个题目初看很简单,如果不要求步数,√2021一定能尺规作图作出来,因为我们可以尺规作出边长为1的等腰直角三角形,其斜边为√2,再以√2和1为直角边作直角三角形,则其斜边为√3,...依此类推,以√n和1为直角边做出直角三角形,则其斜边即为√(n+1),
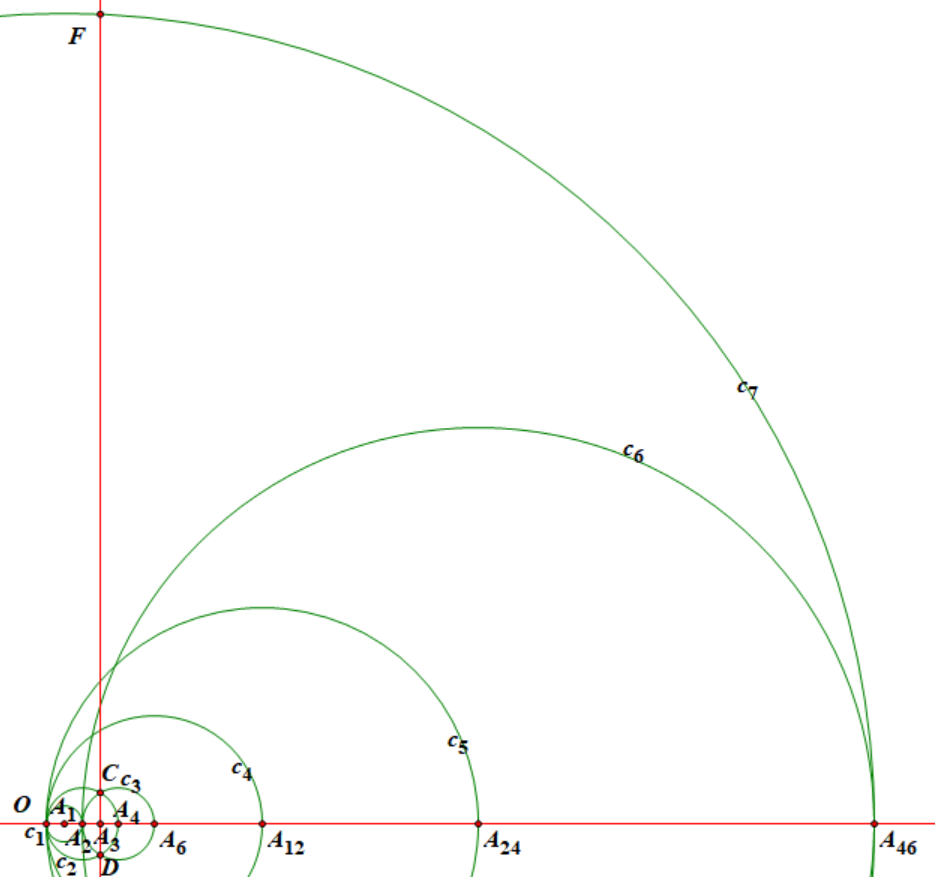
如下图所示,像一个美丽的贝壳。所以首先我们确定了√2021一定能尺规作图作出来的。
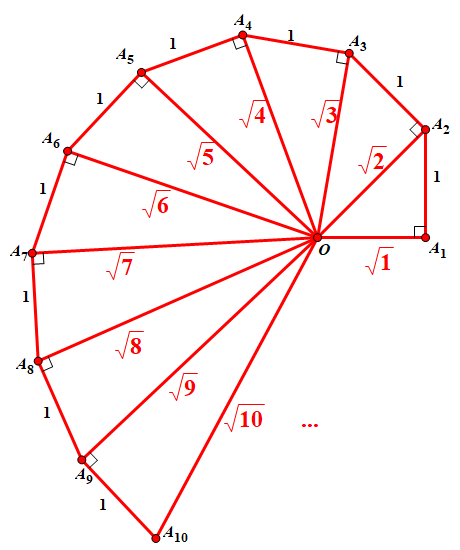 当然,这是一个笨方法,有很多方法可以提高效率,减少作图步骤。为了避免引起争议和混乱,这里需要先明确一下几何中尺规作图有哪些基本步骤,一般是指以下两个:
当然,这是一个笨方法,有很多方法可以提高效率,减少作图步骤。为了避免引起争议和混乱,这里需要先明确一下几何中尺规作图有哪些基本步骤,一般是指以下两个:
(1)经过两点可以引一条直线(或在两点间可以联结线段);
(2)以定点为圆心,图形中某个给定的线段长为半径可以作一个圆(或一段弧)。
下面考虑本问题,如何尽可能快的用尺规作出√2021?
基本的想法当然是将其放到一个其余两边长为整数的直角三角形中。考虑最接近2021的完全平方数,容易知道45*45=2025,从而2021=45*45-2*2是一个最自然的选择。
下面就是两个问题,一个要作出长度为45的线段,还要将其作为斜边,2为一条直角边作出一个直角三角形。
考虑“效率”最高的作线段的方式,即二分法:太极生两仪,两仪生四象,四象生八卦...
即先作半径为1的圆其直径为2,再做半径为2的圆,直径为4,再依次作出8,16,32.
而最快的得到45的方式是45=32+8+4+2+1。如下图所示,其中GH=45.
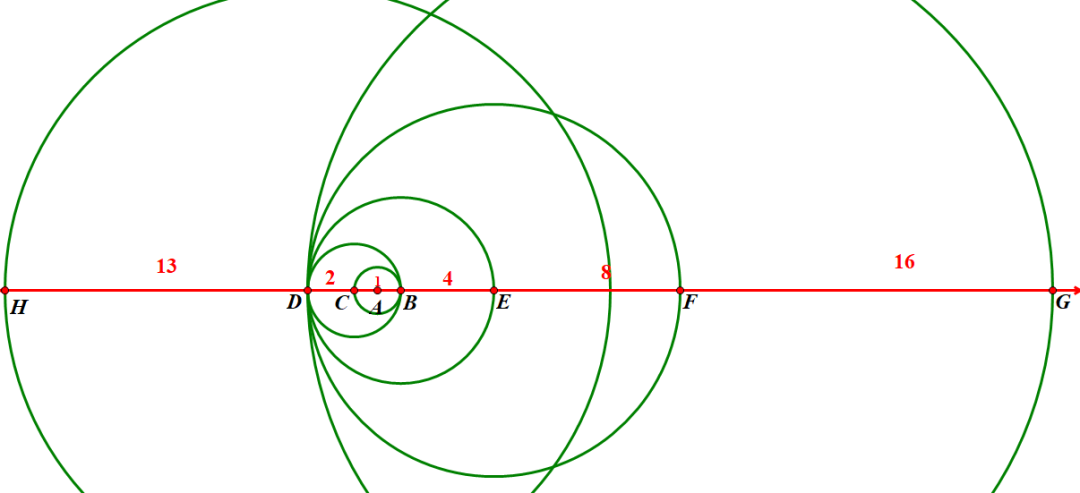
下面考虑如何尽快作出以45为斜边,2为直角边的直角三角形。最容易想到的是作出以45为直径的圆,然后以直径一端为圆心2为半径画圆与此圆交点,此点与另一端点的连线即为所求的√2021。要作以45为直径的圆,需要先作出其垂直平分线得到其中点,这样画出来的图如下所示:
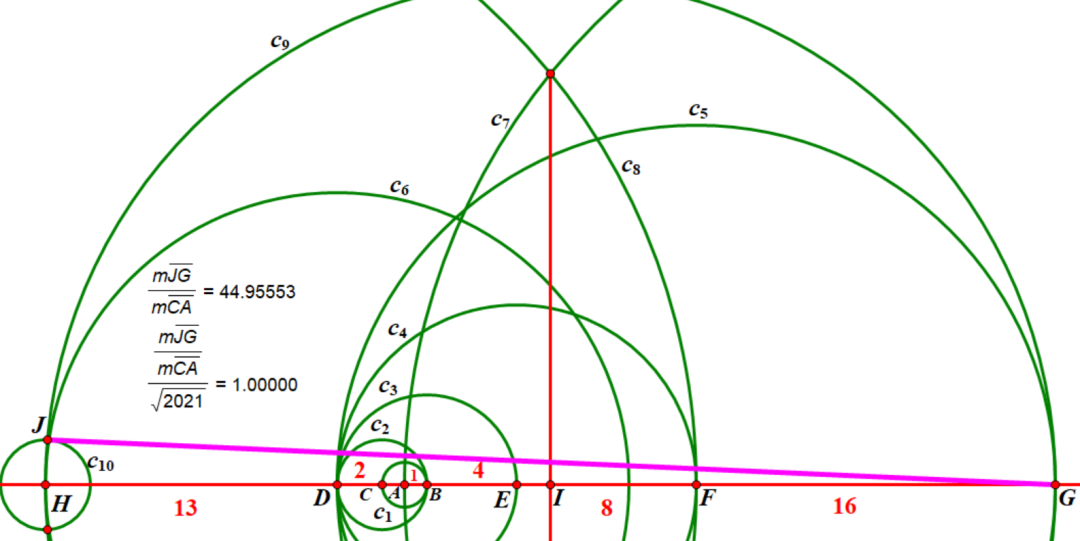 数一下发现用了10个圆和三条直线,即用了13条直线或者圆,题目要求不超过10个圆或者直线,所以不满足条件!
数一下发现用了10个圆和三条直线,即用了13条直线或者圆,题目要求不超过10个圆或者直线,所以不满足条件!
下面考虑上述作法中能否节省一些步骤。感觉前面作到45或者32似乎都有必要,但是后面作以45为直径的圆的时候作中点有点浪费,其实关键就是找到45的中点I,而HI=22.5,故EI=2.5,我们可以以C为圆心1为半径画圆与C1相交,公共弦交AB于K,则DK=2.5,
以E为圆心DK为半径的圆与AB的右边的交点即为I,这样省去了最后的两个圆和一条公共弦,多用了两个圆和一条弦,似乎没有变化!但是这样以来,可以不要点G,也就是说可以省去C5(也可以先不作H,省去C6),如下图所示,这样就能省去一个圆了。
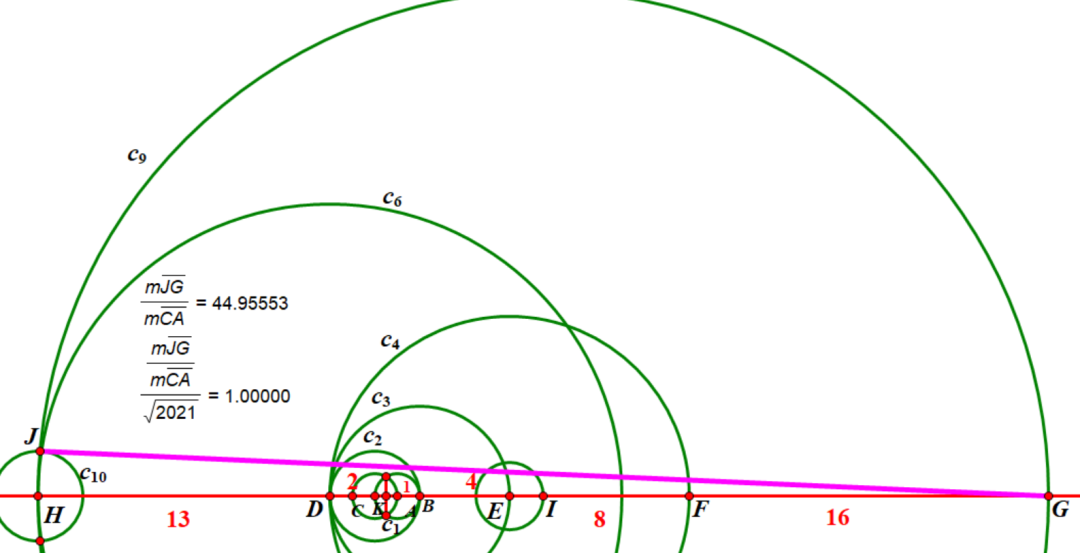 别的地方似乎很难再省去步骤了。
别的地方似乎很难再省去步骤了。
仔细思考一下可以发现,上述作法的关键是作出22.5,不一定要作出45.所以上述作图方法还可以重新改进,尝试尽快作出22.5。既然要出现0.5,不妨最开始就作出来,故以A、B为圆心作单位圆,则得到3,进而得到6,12,24,而22.5=24-1.5,这样按下图作下来用了7个圆和三条线,刚好满足条件!这样就得到了一种满足条件的作图方法,具体作法如下:
 1、作直线AB,设AB=1,
1、作直线AB,设AB=1,
2、分别以A、B为圆心1作单位圆,交AB于另两点D,C,两圆公共弦交AB于O,则CD=3,DO=1.5。
3、以C为圆心CD为半径的圆交AB于E,则DE=6。
4、以E为圆心ED为半径的圆交AB于F,则DF=12。
5、以F为圆心FD为半径的圆交AB于G,则DG=24,OG=22.5。
6、以O为圆心OG为半径的圆交AB于I,则IG=45。
7、以I为圆心BD为半径的圆交大圆于J,则JG=√2021。
上述作法中共使用了7个圆,连了3条直线,故满足条件。
此为解法一。
这样就找到了一种满足条件的作图方法,此解法算是一个自然而直接的解法。上述解法中作出以45为直径的圆的想法最容易想到,但是比较费步骤。一个改进的办法是在AB上作XY=2,以X为圆心45为半径的圆与过Y的AB垂线的交点P,则YP=√2021.
有了这个改进后,最开始那个用了13个直线或圆的作法也能改进.如下图,具体作法为:
 1作直线AB,设AB=1,
1作直线AB,设AB=1,
2以A为圆心作单位圆,交AB于另一点C,则CB=2。
3以C为圆心CB为半径的圆交AB于D,则DB=4。
4以B为圆心BD为半径的圆交AB于E,则DE=8。
5以E为圆心ED为半径的圆交AB于F,则DF=16,AF=13。
6以F为圆心FD为半径的圆交AB于G,则DG=32。
7以D为圆心AF为半径的圆与AB左边的交点为H,则HG=45,
8以E为圆心HG为半径的圆交4中以B为圆心BD为半径的圆于KL,连接KL交AB于J,则BJ=2。
9 以B为圆心AF为半径的圆交JK于P,则JP=√2021。
上述作法中共使用了8个圆,连了2条直线,故满足条件。
此为解法二。
当然上述作法应该还能再改进。上述两种思路估计是最容易想到的,当然还有一些更巧妙的想法。
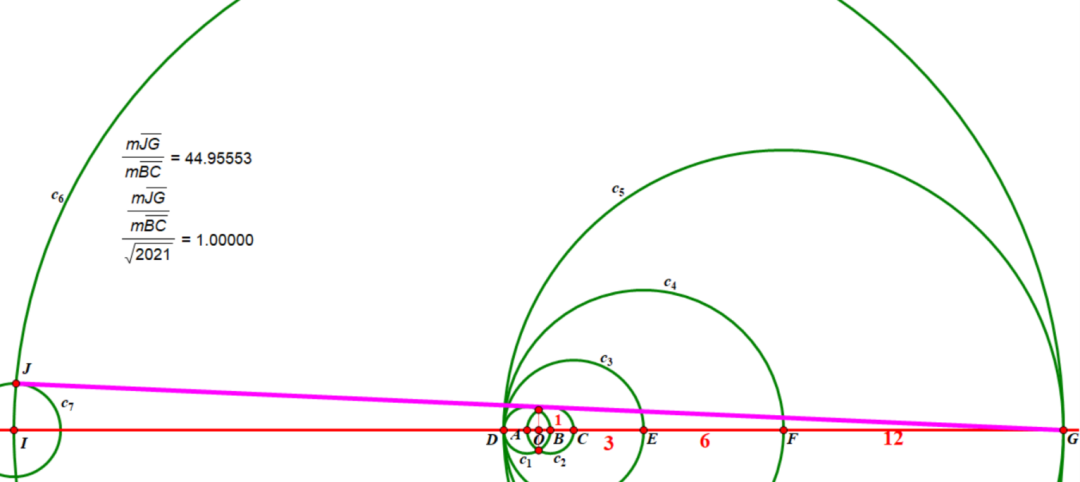
例如陈晨老师,他的大概思路是通过最开始的一条线和6个圆作出45,再作一个半径2的圆的同心圆(半径为45),再以大圆与直线的一个交点为圆心4为半径做圆,其与大圆交点与另一交点的连线与半径2的圆的切点即得√2021的线段。这样刚好用了8个圆和两条线,满足条件。此为解法三。具体解法如下:
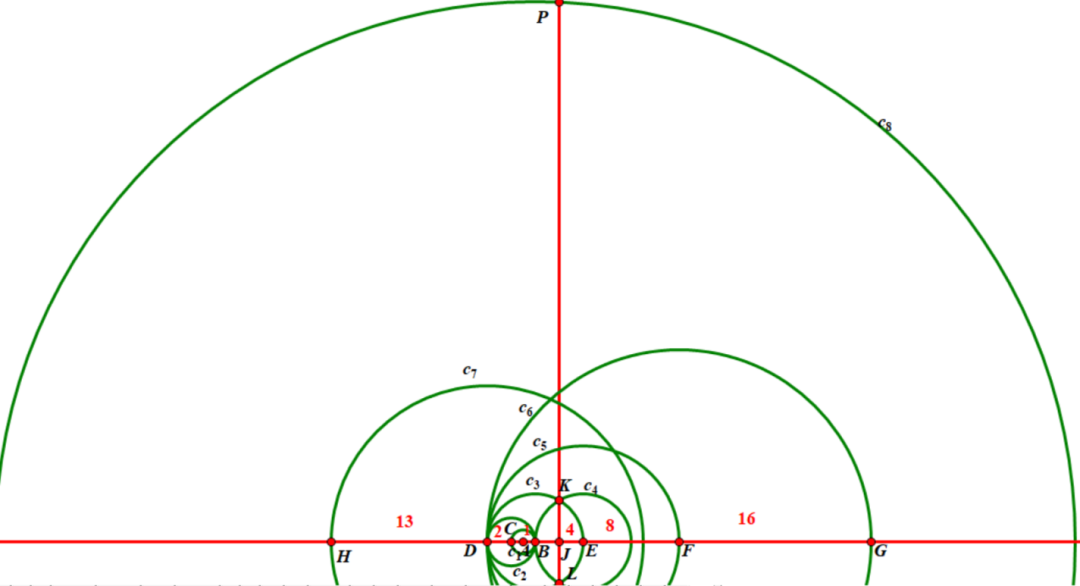
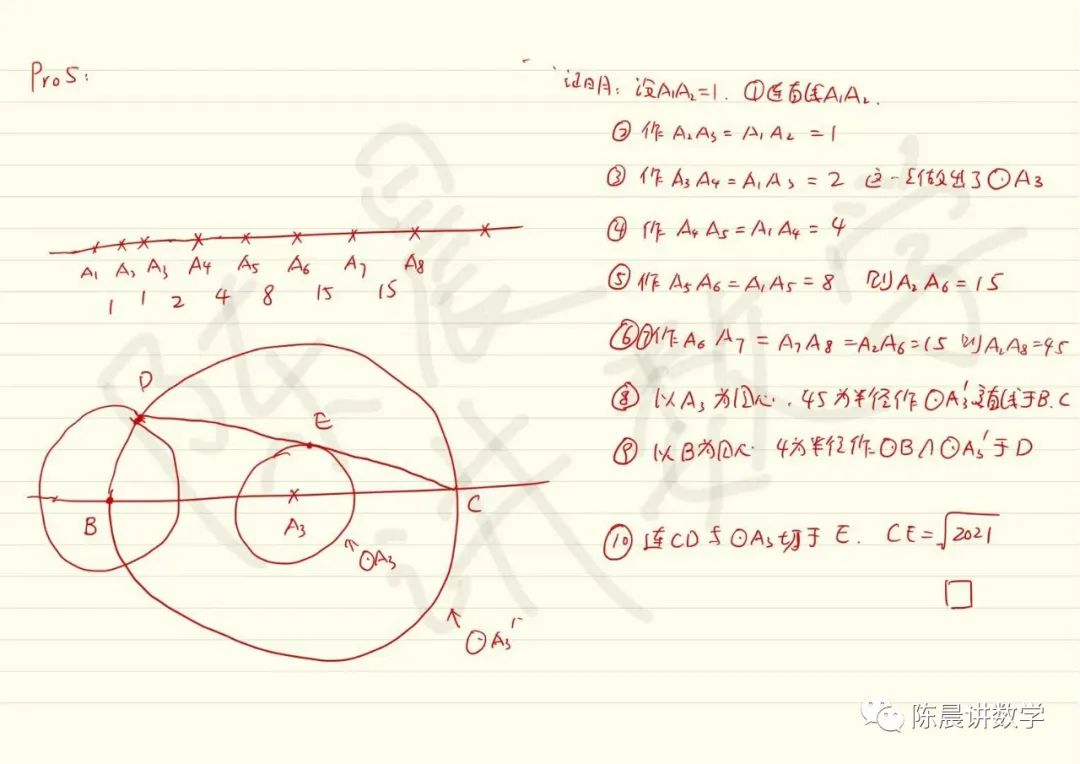 还有猿辅导的解法,其基本思路为作出半径为45的圆,以一个交点为圆心2和4为半径作圆,相当于最后作了两腰为45,底边为4的等腰三角形,其顶点与底边中点的距离即为√2021。此为解法四。具体作法如下:
还有猿辅导的解法,其基本思路为作出半径为45的圆,以一个交点为圆心2和4为半径作圆,相当于最后作了两腰为45,底边为4的等腰三角形,其顶点与底边中点的距离即为√2021。此为解法四。具体作法如下:
 当然上述四种解法都可以有一些变形等效作法。应该还有不少其他的思路也能解决本题。
当然上述四种解法都可以有一些变形等效作法。应该还有不少其他的思路也能解决本题。
下面还有一个“争议性”的问题:以图中某点为圆心,已知线段长度为半径画圆算不算是一个基本步骤?
一般的,在几何中认为算是一个基本步骤。即圆规是我们常用的圆规,可以先量出某一段的长度,然后圆规保持这种状态,再以某点为圆心,此长度为半径画圆。
有时候为了增加难度,可以要求使用“紧规”,即拿起圆规以后,圆规的两脚自动闭合,这样就只能以图中某点为圆心,过另一点作圆。虽然不难证明,在这种限制下,前面的那个作法也能完成,但是要增加一些步骤(可以证明,最少需要5个基本步骤)。
一个自然的问题是:此题用紧规能否在10步内完成?
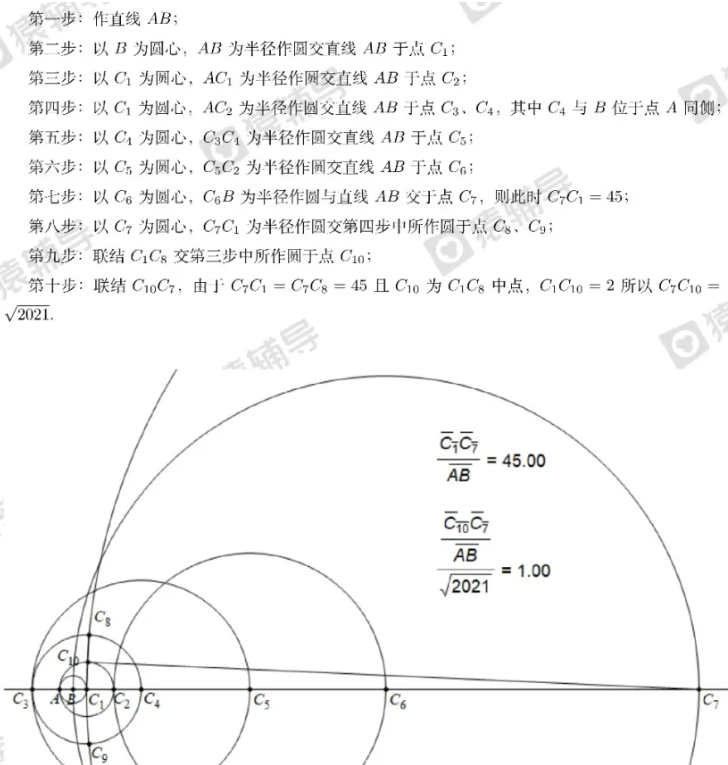
答案是肯定的,而且事实上9步就可以了。其基本思路和解法2类似,大概想法就是将解法2图形中的线段长度扩大2倍,最后一步圆稍小一点即可直接作出45,从而即可完成作图。我看到单墫单老、爱尖子平台、质心网等都是此种解法。估计参考答案给出的也是此种解法。具体图形和作法如下:
 上述9步,每一步是一个基本步骤。此为解法五。
上述9步,每一步是一个基本步骤。此为解法五。
所以本题简单易懂,入手点很多,解法估计也是五花八门,近500名考生中估计有几十种解法。
上述五种解法显然第五种最简洁也最优美。不过如果本题要求使用紧规,最多使用9个基本步骤,可能只有上述第五种解法满足。那此题的难度将大大提升。估计命题组为了降低难度,放松了要求,最终题目呈现如上。
据说本题最后的评分标准如下:
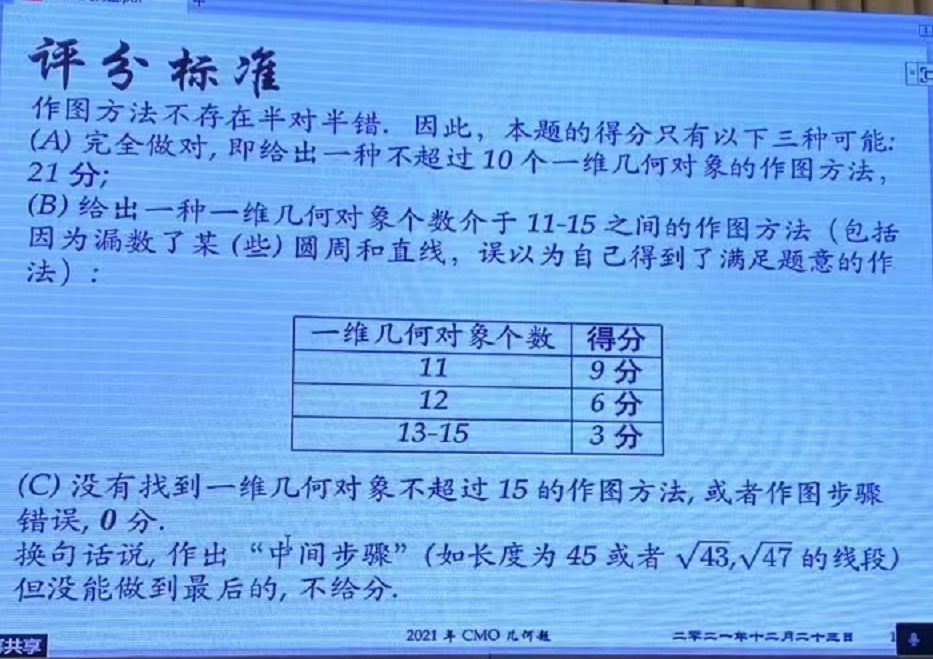 学生虽然对尺规作图不是很熟悉,但是本题容易上手,学生答的还是很好的,据说平均分15分多。所以此题引起了老师和学生的不少争议。
学生虽然对尺规作图不是很熟悉,但是本题容易上手,学生答的还是很好的,据说平均分15分多。所以此题引起了老师和学生的不少争议。
这样从结果来看,作为第二题本题的难度有点低,说明命题组对此题难度的估计不够准确。平心而论,竞赛题的难度本来就非常难以估计,命题组专家们的评估可能最终结果大相径庭也是司空见惯的事情。另一方面,所谓长江后浪推前浪,一代更比一代强。这个结果也反映出竞赛学生的数学水平和以前比有了显著的进步。
不过我觉得瑕不掩瑜,本题是一个很好的题目。一方面命题老师希望通过考察此题引导大家对几何的基本能力——作图的重视,确实尺规作图问题既经典又深刻,初看简单明了,引人入胜,古希腊人就有了深入的研究,也提出了很多未曾解决的问题;然而严格证明其中的结论却需要近代的代数、数论、群论等知识,因此她是一个数形结合的完美产物,可以说尺规作图能够综合考察数学竞赛的四块内容:几何、代数、数论、组合。另一方面,本题简单易懂,初一、初二的学生都可以尝试解决本题。而且题目的设计梯度合适,入手点很多,解法也非常多,所以区分度还是不错的。还有考察尺规作图算是突然袭击,几乎大家都估计不到,也基本上不会培训到。这样能够更加真实的反应学生的几何素养,而和赛前及平时的培训的关系就不太大了。
当然这次CMO的题目每题都有梯度,难度整体也都不太高,平均分66.6(满分126分)也是历年最高的。我觉得这是一个好趋势,因为参加CMO的人数越来越多,平均分在50%附近区分度是最高的,能够真实的反应学生的数学水平的差距。
当然上述解法只是说明9个基本步骤能够作出√2021。是否还能更少?如果不能,应该如何严格证明,都是一个很有挑战性的问题。
不少老师感觉此题考察一个特例√2021的尺规作图太简单,而且无法反应此类问题的研究过程,可以考虑考察一般的作图√n的尺规作图的最少步骤问题。
一般性的问题为:已知平面上两个点A,B,且AB=1,并尺规做出一条直线上两点,使得此两点的长度为√n,最少需要几步?其中连直线和画圆(以图中一点为圆心画过另一点的圆)都各是一步。
估计可能因为此一般性的问题难度太高,不适合作为竞赛题考察。例如我们可以考察几个最初的情况。例如√2的作图最少需要几个基本步骤,这都是一个很有挑战性的问题,有兴趣的读者可以挑战一下,这里我先卖个关子,不公布答案了。常见的作法是6步,其实5步就能作出来。
我得到的√1,√2,√3,√4,√5,√6的最少步骤分别是1,5,3,2,6,6。我在著名的在线整数列网站(OEIS)(http://oeis.org/)上查找了一下,好像没有找到此数列。可能我算错了,也可能我的定义不太合理,和其他人的定义不同,结果也会有差异。当然也有可能此类问题还没有被OEIS网站收入。
其实看到此题,我就想到了一个作图游戏《欧几里得(Euclidea)》,此游戏点开后背景就是欧几里得拿着尺规在思考。这是一款尺规作图游戏,而且是使用“紧规”,要求用最少的步骤完成作图。
 很多人也觉得本题是受此游戏启发编制的,玩过此游戏对解决本题是很有帮助的。所谓有心栽花花不成,无心插柳柳成荫。我们学习也不需要过分的功利,有时候适度放松,玩玩数学游戏对数学学习也是大有裨益的。
很多人也觉得本题是受此游戏启发编制的,玩过此游戏对解决本题是很有帮助的。所谓有心栽花花不成,无心插柳柳成荫。我们学习也不需要过分的功利,有时候适度放松,玩玩数学游戏对数学学习也是大有裨益的。
这个游戏的挑战性相当大,用尺规作出结果不难,但是要用最少的步骤却殊为不易。例如刚才提到的√2的作图其实本质就是其中第一大关的第7小关用7个基本步骤(7E)作出圆的内接正方形。
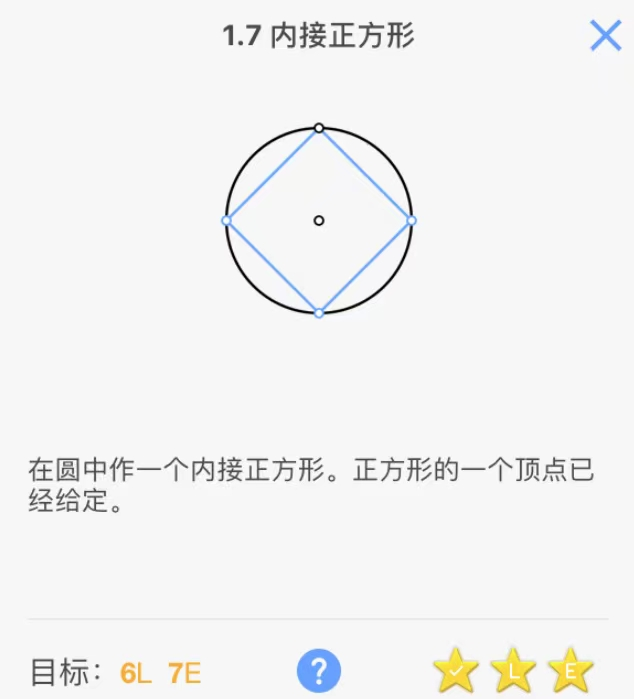
我一般给竞赛的学生讲几何的时候都会推荐他们玩这款游戏,我也玩了很久这个游戏。当然此游戏的难度颇高,很难通关。对于几何刚入门的学生,推荐另一款比较简单的游戏《毕达哥拉斯(Pythagrea)》,图标如下,这个适合初学几何的学生,甚至小学生也能玩。

我以后有空了准备写个《玩游戏,学几何》系列,写写这些几何游戏的攻略和作法及证明以及互相之间的联系。













