2022年西交大少年班数学试题

已知，，则的值为___________．
已知点，为轴上的一动点，为切线，已知圆半径为，则的最小值为___________．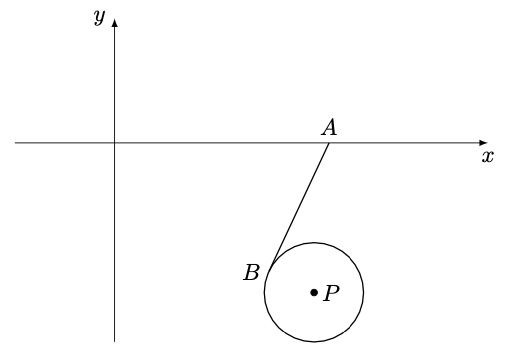
，，为该方程两根．则的值为___________．
已知矩形，，．为上一动点沿翻折，当为直角三角形时，的周长为___________．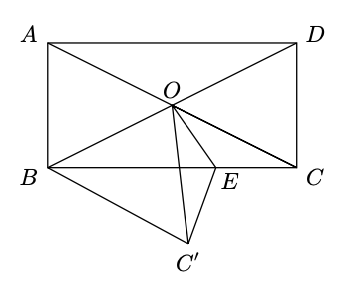
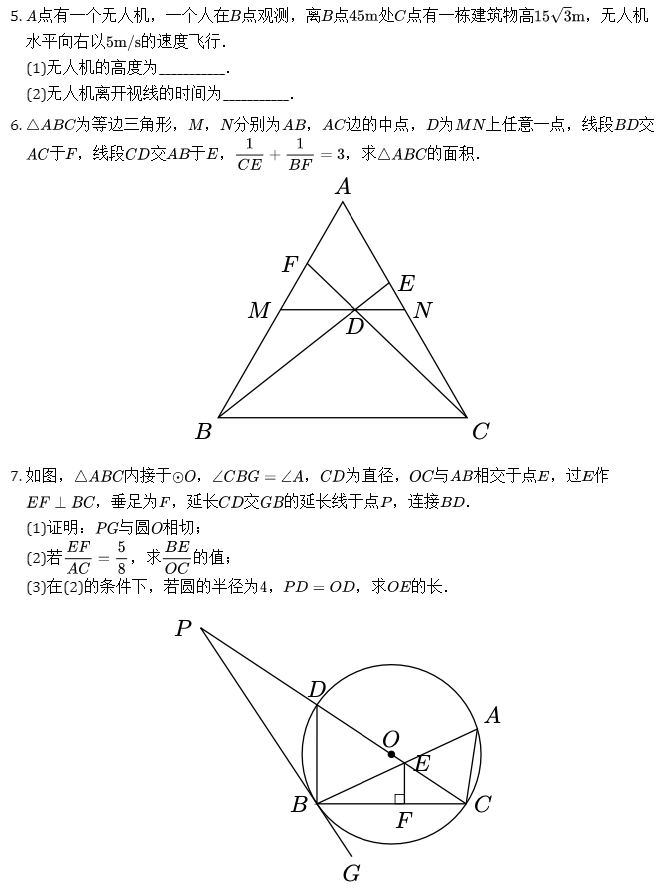
点有一个无人机，一个人在点观测，离点处点有一栋建筑物高，无人机水平向右以的速度飞行．
(1)无人机的高度为___________．
(2)无人机离开视线的时间为___________．
为等边三角形，，分别为，边的中点，为上任意一点，线段交于，线段交于，，求的面积．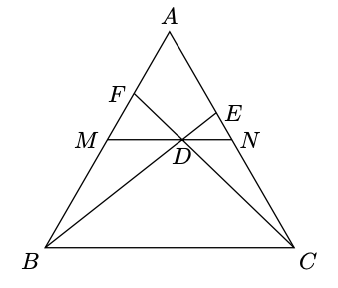
如图，内接于，，为直径，与相交于点，过作，垂足为，延长交的延长线于点，连接．
(1)证明：与圆相切；
(2)若，求的值；
(3)在(2)的条件下，若圆的半径为，，求的长．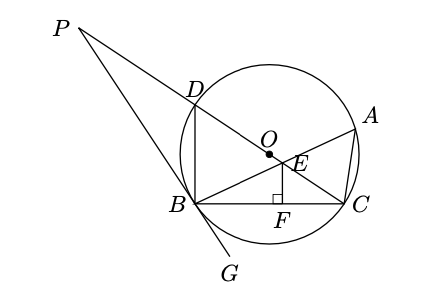
已知函数．
(1)证明：函数与轴恒有交点；
(2)证明：无论为何值，函数必过一定点；
(3)设函数图像和轴交点为，顶点为．若，将函数沿方向平移，和一定点与原顶点所连线段有交点，求平移后顶点横坐标的范围．
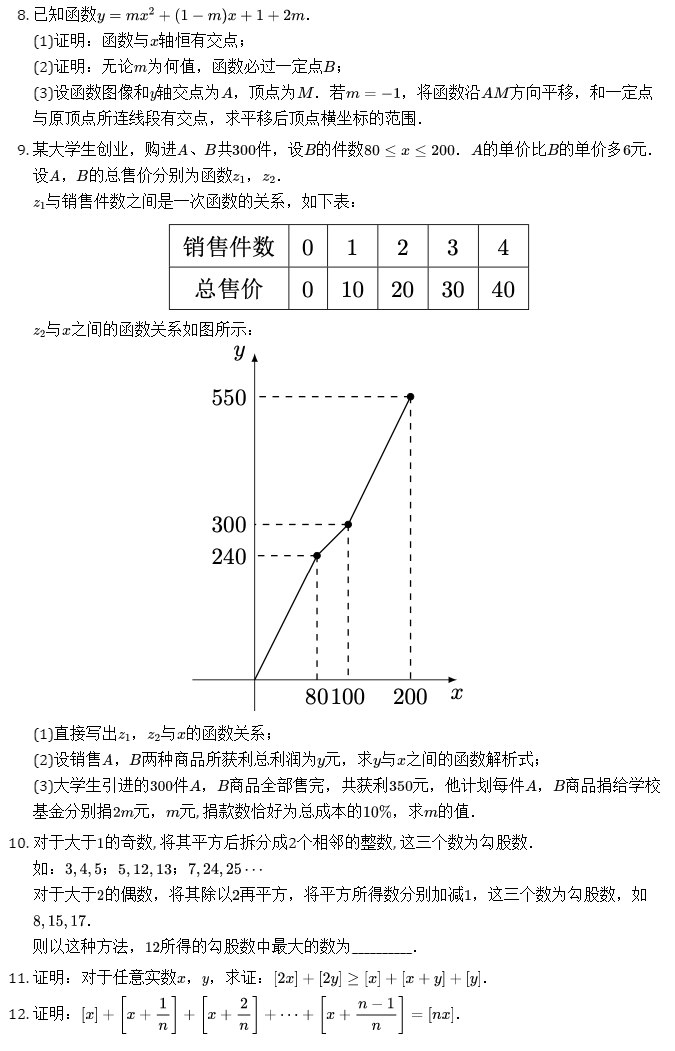
某大学生创业，购进、共件，设的件数．的单价比的单价多元．设，的总售价分别为函数，．
与销售件数之间是一次函数的关系，如下表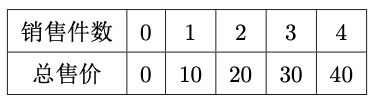：与之间的函数关系如图所示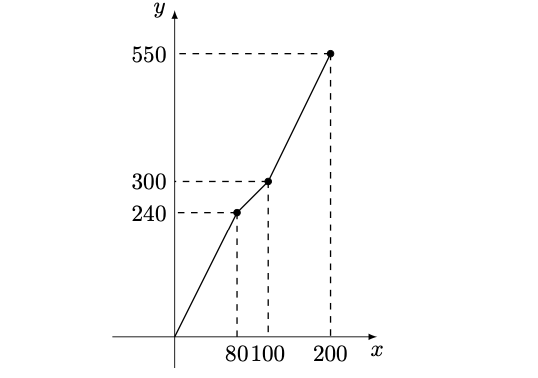：(1)直接写出，与的函数关系；
(2)设销售，两种商品所获利总利润为元，求与之间的函数解析式；
(3)大学生引进的件，商品全部售完，共获利元，他计划每件，商品捐给学校基金分别捐元，元, 捐款数恰好为总成本的，求的值．
对于大于的奇数, 将其平方后拆分成2个相邻的整数, 这三个数为勾股数．
如：；；
对于大于的偶数，将其除以再平方，将平方所得数分别加减，这三个数为勾股数，如．
则以这种方法，所得的勾股数中最大的数为__________．
证明：对于任意实数，，求证：．
证明：．