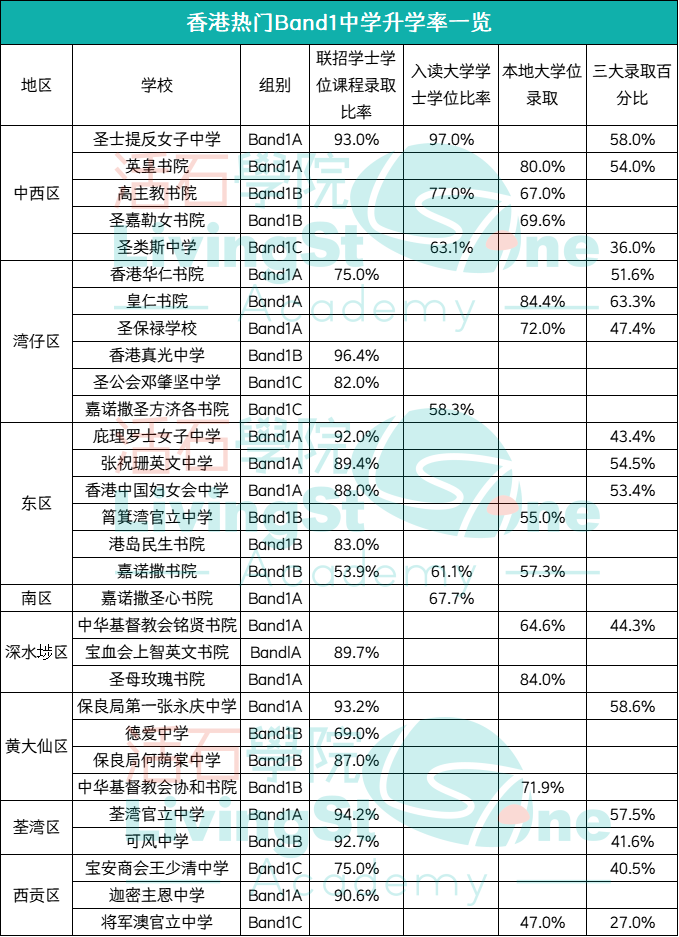
今天为大家带来的是一道关于电阻并联和电阻率的题，物理原理并不难，难度还是在数学计算上。如何在规定时间内，又快又准地把题目算对，是 BPhO 对每个参赛学生的考验。下面接题吧：
e) Figure 1 shows the cross section of a high voltage overhead electrical transimission cable. The central strand is of steel and the six outer strands are of aluminium. The resistivity of steel is 
, and that of aluminium 
. The cross-sectional area of each strand is 
. The steel is present to give mechanical strength to the cable and only reduces the resistance of a length l of cable by 
when it is included. Calculate the length of the cable. [5 marks]
答案解析：
题目告诉我们输电线是由 6 条铝线和中间 1 条铁线组成的，铁线是为了加固输电线的硬度。铁线的存在会使长度为 l 的输电线电阻减少。又告诉了铝和铁的电阻率 (resistivity) 和电线横截面积 (cross-sectional area)，让求输电线的长度 l。
本题首先需要明确的一点是，这 6 条铝线和 1 条铁线是并联关系，所以它们的总电阻符合如下并联公式：
既然涉及到电阻和电阻率，就要用到它们之间的关系式：
式中 R 为电阻 (resistance)，ρ 是电阻率 (resistivity)，L 代表电阻的长度 (length)，A 代表电阻的横截面积 (cross-sectional area)。
加入铁线以后，会使整个电线的电阻减少 
，我们接下来以这个已知为突破口，先算出没有铁线、和有铁线两种情况下的阻值，再将两者相减。
没有铁线时，是 6 条铝线并联，其中每一条铝线的阻值是：
那么 6 条铝线的总电阻 R 是：
式中铝的电阻率 ρAl 和每根电线的横截面积 A 均为已知，但我们也不着急代数计算，可以先表示成物理量的关系式放在这里、比较好看。
中间加入铁线以后，就是在上式的基础上再并联一个铁线的电阻。先给出铁线电阻的表达式：
式中的铁线长度 l 和横截面积 A 均和铝线的相同，铁线电阻率 ρFe 为已知。
所以加入铁线后，总电阻 R' 为：
现在我们有了 R 和 R’ 的表达式，题目中又已知两者差值为 
，所以可列等式、代数运算后即为本题答案：
可见，最后这几步公式推导、代数运算对数学计算能力要求高。其实如果在前面求铝线和铁线各自的电阻时就早点儿代数运算，反而计算过程会简单一些。
【竞赛报名/项目咨询+微信：mollywei007】
