今天来做一下 c) 和 e) 问，把它俩放一起是因为两问都是研究地球内部的情况，物理原理相对简单，但计算确实复杂，建议找一个头脑清醒、有充裕时间的早晨来研究这两问。
Section 2 试卷中每道大题 25 分，可分配时间为 40 分钟，也就是 1 分值的题对应大约 1.6 分钟。这两道小题一共 7 分，对应时间大约是 11 至 12 分钟，在这么短的时间内做完是个很高的要求。在我看来，能做出来就已经不错了；如果控制在 15 分钟左右，更好。
c) The density of the Earth changes sharply between the core and the mantle. By taking just two suitable values of the density of the core and mantle of the Earth from the graph in Figure 1, estimate a value of the mass of the Earth using this data. Your values and calculation must be shown.
(3)
e) The Earth can be considered to consist of concentric spheres of material, the outer sphere being the crust with a density of 
. If the mass of the Earth is 
, what will be the fractional change in the gravitational field strength when descending to the bottom of a gold mine, a distance d = 3000 m below the surface of the Earth?
Hint: the field inside a hollow spherical shell is zero.
(4)
答案解析：
c) 问运用的物理原理非常简单，就是物体质量 m 等于其密度 ρ 乘以体积 V，只不过这道题是涉及到地幔 (Earth Mantle) 和地核 (Earth Core) 的概念，如下图：
地核 (Earth Core) 是位于地球中心的球体，而地幔 (Earth Mantle) 是包裹在地核外的一个厚厚的球壳。在求解地球总质量时，我们近似认为地球是由地核和地幔组成，忽略地壳 (Earth Crust) 的影响。
首先，我们关注地核部分 (Earth Core) 的质量，如下图所示：
通过上图进行数据估读，由竖直的辅助虚线可以看出，地核部分的半径大约是 3500 km；整个地核的密度不均匀，但由水平的辅助虚线可以看出，平均密度大约在 
。有了球体半径，可求球体体积；又有了密度，就能求出整个地核的质量：
再来分析一下地幔 (Earth Mantle)，它是包裹在地核外部的厚球壳，从题目中所给的图来看，地幔的密度是小于地核的：
由上图水平虚线可看出，地幔的平均密度大约是 
; 两条竖直虚线表明地幔的半径跨度是从 3500 km 到 大约 6300 km。
由于地幔是个厚球壳，其体积的计算方法是用地球的总体积减去内部地核的体积，即：
那么地幔质量就是：
地球质量则是地核和地幔质量的加和：
由于这是道估算题，答案在 
之间都算对，而地球的真实质量是 
，说明以上方法估得比较准确。
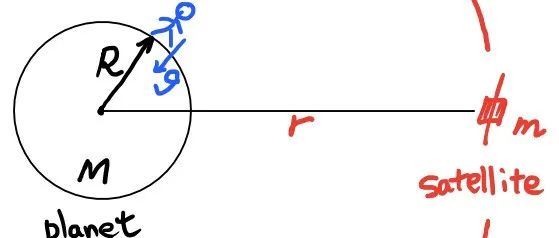
e) 问求地表下面 3000 m 处金矿的引力场强 (gravitational field strength) 相对于地球表面引力场强的变化比例，我们先将题目描述的情况做如下图：
图中 Gold 即为金矿所在地，在地表以下 d = 3000 m 的位置处。我们设地球半径为 R，注意地球半径是竞赛试卷的已知常数之一：
那么图中金矿距离地心 O 就表示为 R - d，R 和 d 都是已知。
本题非常重要的已知是 Hint: the field inside a hollow spherical shell is zero. 对于一个球壳来说，其内部的引力场强处处为零！
为什么要给出这个已知？
由于上图中的 Gold 位于地球内部，为了求此位置的场强，我们以 O 为圆心，以 R - d 为半径，把地球划分为两个区域：一个是图中半径以外的蓝色区域；另一个是半径以内的绿色区域。
对于蓝色区域来说，它就是一个球壳，已知又暗示了球壳内部重力场强处处为零，所以这个区域在 Gold 处合场强为零！
于是简化为求绿色区域的球体在 Gold 处的引力场强，球体表面的引力场强公式不难推导出，有：
上式中 g' 即是 Gold 处的引力场强，G 是万有引力常数，M2 为绿色区域的质量（目前未知），分母中的 R 和 d 都是已知。
由于要和地球表面的重力场强 g 相比较，所以同样的方法推一下地球表面的重力场强：
类似推导在本大题 a) 问中也用过，应该比较熟练了。上式中 g 即是地球表面的引力场强，M 为地球质量，分母中的 R 是地球半径，均为已知。
所以 e) 问中要求的 fractional change 可表示为：
式中物理量除了 M2 、均为已知，求出 M2 本题就迎刃而解了。
现在已知地球总质量 M 和蓝色区域的密度 ρ，有了密度、再求出蓝色区域球壳体积，相乘、就有质量 M1 :
再用地球总质量 M 减去蓝色区域的质量 M1 就可得到绿色区域的质量 M2 ：
发现 M1 相对于地球质量 M 来说微不足道，所以 M2 和 M 的质量就很接近。将这里求得的 M2 和其他已知代入到上述 fractional change 的表达式中，代数计算即为本题结果：
可见地下 3000 米的金矿引力场强和地球表面相差无几，主要是因为 3000 米相对于地球的半径实在是微不足道。
e)问计算量相当大，而却只有 4 分的分值，考试中如果时间紧张，建议先把公式、方法写出来，拿到方法的分儿，后续有时间的话再进行计算。
BPhO 标准答案中强调了 3000 米远小于地球半径、以至于可以忽略 3000米来近似计算，过程确实简单许多，但作者认为该方法并不完全合理，所以没有采纳。
【竞赛报名/项目咨询+微信：mollywei007】
