2022年数学建模国赛C题思路解析

2022年国赛C题相对于其他题目而言比较简单，因此去年选择C题的队伍更多，如何在众多论文中脱颖而出？这需要相比其他队伍更优的模型和求解方法以及更清晰的行文逻辑。让我们一起来看看去年的国赛C题吧！

原题重现

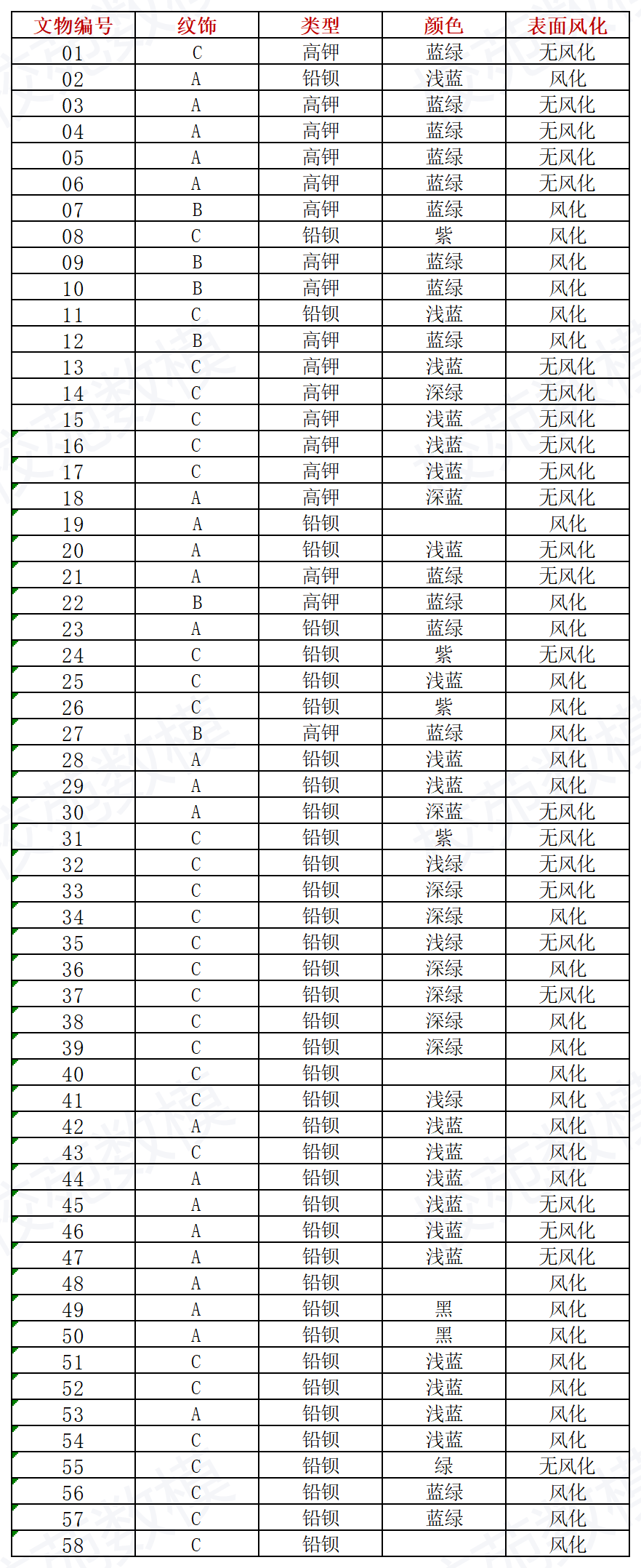附件表单1

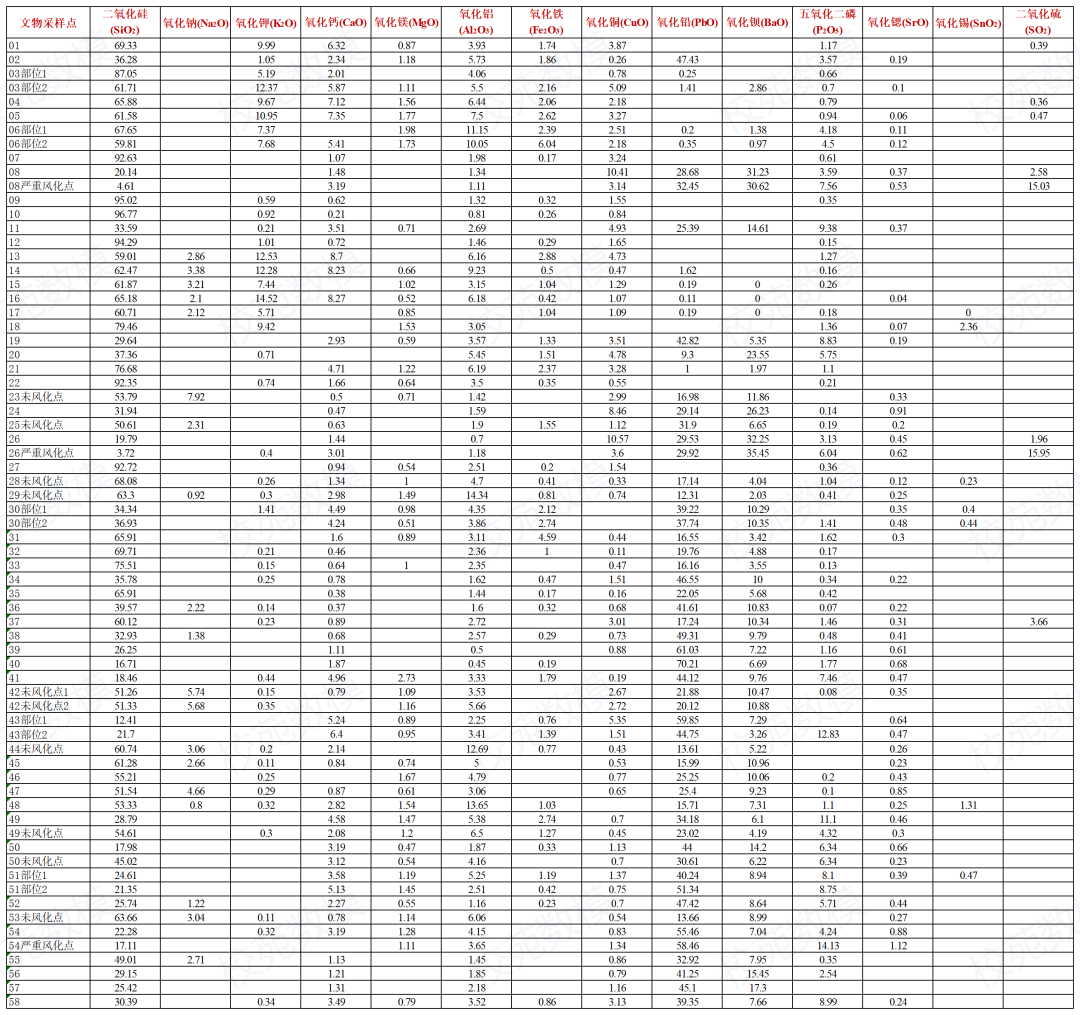
附件表单2

附件表单3

评阅要点

本题通过对古代玻璃制品的化学成分数据分析，研究有无风化玻璃制品成分的变化规律，以及高钾、铅钡两种玻璃类型的化学成分统计规律，并探索亚分类的方法，进而可以依据未知分类的文物化学成分对文物进行准确的分类。

本题数据的主要特点是成分性，即各化学成分比例的累加和应100%，具有定和约束，在统计学上称为“成分数据”。同时由于定和约束，成分数据各变量之间具有明显的共线性，使得常规的统计分析方法失效。通常需要通过适当的变换解决这类问题，比如:中心对数比变换(CenteredLog-ratio,CLR)等。

问题 1

对玻璃文物表面风化与其类型、纹饰和颜色的关系进行分析，这是离散变量和连续变量的相关性分析、由风化点和未风化点的检测数据预测其风化前的化学成分含量的问题，需要分析风化与未风化两个总体的统计规律，通过总体之间的匹配进行预测。

(1) 数据预处理:无效数据去除，应避免对有效数据的删除;数据误差修正。

(2) 如果使用卡方检验，应注意其适用条件。

(3)于没有风化前后匹配的数据，采用简单的线性回归模型是不合适的。

(4) 应该充分考虑到成分数据的特点，简单地取均值不满足成分性的约束。

问题 2

依据表单1、表单2 数据，分析高钾玻璃、铅钡玻璃的分类规律，这是一个有监督的分类问题:亚类划分是一个无监督分类问题:敏感性分析是考察分类方法的稳定性。

(1)按高钾、铅钡两大类或者按四类(高钾无风化、高钾风化、铅钡无风化、铅钡风化)进行分类规律的讨论均可。

(2) 对分类效果应给出相应的评价;对亚类划分结果应能明确阐述其亚类特征，解释其重要成分。

(3) 鼓考虑成分变量的选择对分类结果的影响。

(4) 应该充分考虑到成分数据特点，关注样本之间距离的合理性。

问题 3

对附表单3中未知类别玻璃文物的化学成分进行分析，鉴别其所属类型，这是一个判别问题。敏感性分析是考察判别方法的稳定性。

(1)基于高钾、铅钡两类或者按四类(高钾无风化、高钾风化、铅钡无风化、铅钡风化)进行判别均可。

(2) 应该充分考虑到成分数据特点，关注判别方法的合理性。

问题4

针对不同类别的玻璃文物样品，分析其化学成分之间的关联关系，并比较不同类别之间的化学成分关联关系的差异性，这是一个化学成分的相关性分析问题。

针对不同类别的玻璃文物样品，分析其化学成分之间的关联关系，并比较不同类别之间的化学成分关联关系的差异性，这是一个化学成分的相关性分析问题。

注：

(1)该问题是一个小样本的统计分析问题，应注意机器学习方法的适用性。

(2)对围绕成分数据特点来研究问题的，应该重点关注，鼓励加分。

思路解析01问题一

壹、数据的预处理

⑴剔除异常值

由于题目将成分比例累加和介于 85%~105%之间的数据视为有效数据，因此对表单2与表单3的成分比例加和，剔除不介于 85%~105%之间的数据。

⑵剔除无效数据

由于玻璃易受风化影响，会影响到对种类的判断，因此将表单中无颜色标注的数据剔除，视为无效数据。

⑶处理空值

为了简化建模，将空值均视为0处理。

贰、建模方法

首先，题目要求对这些玻璃文物的表面风化与其玻璃类型、纹饰和颜色的关系进行分析，因此可以选择利用卡方检验对玻璃文物的表面风化与这三者做相关性分析，根据得出的结论对风化与否做出分类的判断，并得出体现风化的具体元素指标。在这一步推荐使用SPSS,可以避免求解代码，对于编程能力欠缺的队伍十分友好。

其次，利用灰色关联分析判断表面风化程度与各化学元素的关联程度，根据结果将表面风化大致分成高钾风化、高钾未风化、铅钡风化和铅钡未风化四类，对这四类数据分别求取平均值，绘制风化前后的折线图，探究风化前后元素变化，得到统计规律，对于预测，利用风化前后的均值数据做差得到理想差值，后将实际风化后的化学成分含量减理想差值即得风化前各化学成分含量。

02问题二

首先，对数据进行处理，分别筛选高钾玻璃和铅钡玻璃纹饰和颜色情况从而进行分类。 然后，使用典型相关性找出对高钾玻璃和铅钡玻璃影响比较大的元素。根据各元素含量可以制定一个判定高钾玻璃和铅钡玻璃的界限标准，由此将玻璃划分为高钾玻璃和铅钡玻璃，这个标准建立的依据可以考虑相关系数正负，从而写出计算方法。 为了对于每个类别选择合适的化学成分对其进行亚类划分，第一步，需要找出主要元素，选择主成分分析法和因子分析法都是不错的选择。第二步，利用主要元素含量与类别内的数据进行聚类分析，完成亚分类。最后，可以利用 ROC 曲线对亚分类的合理度和敏感度进行分析。

03问题三

由于需要预测未知类别玻璃的类型，这里首先考虑多元线性回归模型对表单 3 的玻璃类型进行预测，以SiO2为因变量，其他元素为自变量进行多元回归，将实际值和预测值进行比较，即可得到表单3的玻璃类型。利用决策树模型学习问题二的分类结果，得到每个类别下的亚分类。再根据灵敏度分析公式R=TP/ (TP+ FN)，得到模型敏感性。

04问题四

利用灰色关联度分析可以得出高钾玻璃和铅钡玻璃对于哪些微量元素的差异性较为明显；然后利用卡方检验和方差检验比较不同类别之间的化学成分关联关系的差异性。

模型假设

①严重风化点和风化点对模型的影响不相同；

②样本数据足够支撑模型的建立与求解；

③玻璃的化学成分种类只含有附件中所给 14 个；

④表中空白处一定是未检测到该成分，并且值为 0。

注意事项

对于国赛C题，常考察统计方法、分类模型、预测模型以及评价模型。对于统计方法，建议同学们至少掌握描述性统计、P值检验、卡方检验和方差检验。分类模型和预测模型，可以适当考虑机器学习部分的模型，比如决策树、BP网络等。

评价模型大家可以考虑TOPSIS、模糊综合评价、主成分分析、灰色关联分析等。但是，一篇国赛论文不是模型越多越好，最重要的还是能解决问题，切记不能让老师产生模型堆砌的感觉。