2022年数学建模美赛C题
--Data Paralysis? Use Our Analysis!

背景
市场交易员经常买卖波动性资产,目的是收益最大化。每一次买卖通常都会产生一笔手续费。黄金和比特币是其中两种波动性资产。
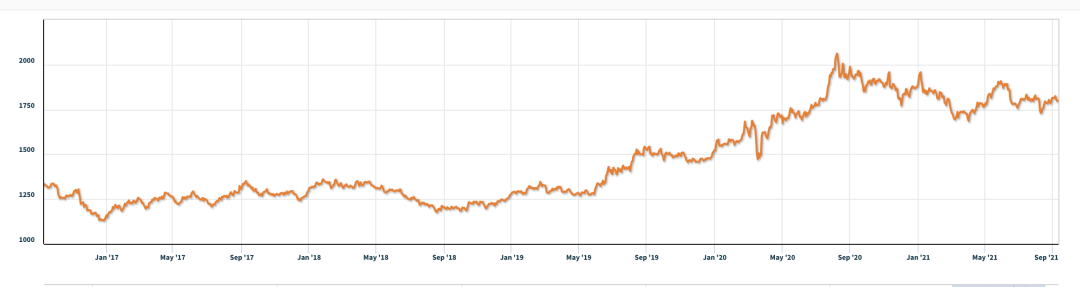
图 1:黄金日价格(美元/盎司)。资料来源:伦敦黄金市场协会,2021 年 11 月 9 日
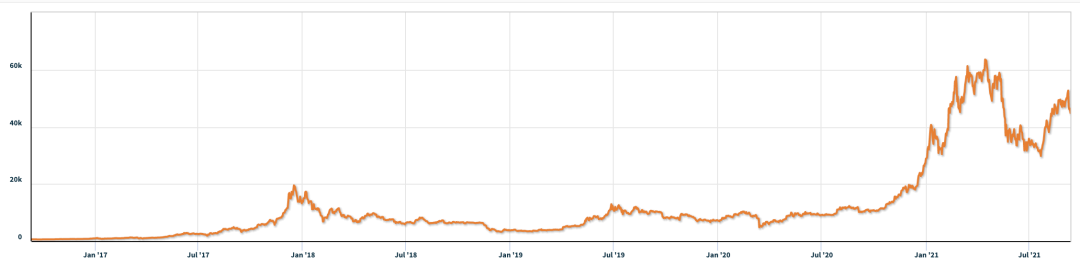
图 2:比特币每日价格(美元/比特币)。
资料来源:纳斯达克,2021 年 11 月 9 日

要求
交易员要求你们建立一个模型,该模型仅使用过去的每日价格来确定交易员每天是否应该买入、持有或出售其投资组合中的资产。
你于 2016 年 11 月 9 日以 1000 美元开始。您的交易期为五年,从 2016 年 11 月 9 日至 2021 年 10 月 9 日。在每个交易日,交易员将有一个投资组合,包括现金、黄金和比特币 ,单位分别为美元、盎司和比特币。三种资产初始持有量为 。每笔交易(买或卖)的手续费成本为交易金额的 %。假设= 1%, = 2%。持有资产没有成本。
注意,比特币可以每天进行交易,但黄金只在开市的日子进行交易,详见价格数据文件 LBMA-GOLD.csv 和 BCHAIN-MKPRU.csv。
建立模型过程中,你们只能使用本题所提供的两个电子表格中的数据,即 LBMA-GOLD.csv 和 BCHAIN-MKPRU.csv
开发一个模型,仅基于截止到当天的价格数据,给出每日最佳的交易策略。通过使用你的模型和策略,给出 1000 美元的初始投资,到 2021 年 10 月 9 日时的资产价值?
提供证据以证明您的模型为最佳策略。
确定该策略对交易成本(手续费)的敏感度。即交易成本是如何影响策略和结果的?
与一份两页以内的备忘录,向交易员展示你们的策略、模型和结果。
最终提交的 PDF 论文的总长度不要超过 25 页,并且应包括:
▲一页摘要
▲目录
▲完整解题方案
▲1~2 页的备忘录
▲参考文献列表
注意:MCM 比赛的参赛论文有 25 页的限制。你们队提交的论文中所有内容(包括摘要、目录、参考文献和任何附录)需控制在 25 页以内。论文中所用到的(别人的)想法、图片和以及任何其他材料都需要注明来源。


附件
提供的两个数据文件包含了解决此问题的唯一数据。
LBMA-GOLD.csv
BCHAIN-MKPRU.csv
数据描述
1、LBMA-GOLD.csv
日期格式:mm-dd-yyyy(月-日-年)
美元(PM):指定日期每盎司黄金的收盘价(单位:美元)
2、BCHAIN-MKPRU.csv
日期格式:mm-dd-yyyy(月-日-年)
价格:指定日期单个比特币的价格(单位:美元)
解题思路与问题分析
市场交易者频繁买卖波动性资产,目标是最大化他们的总回报。每次买卖通常都会有佣金。两种这样的资产是黄金和比特币。您需要开发一种模型,该模型仅使用迄今为止的每日价格流来确定交易员每天是否应该购买、持有或出售其资产配置。
问题一共四问,抛开最后的建议信不谈那就是三个子问题。而问题二是验证问题一结论的正确性,问题三是对问题一结果的灵敏性检验,所以只需要破解问题一即可破解整个问题。问题一是需要我们求解在2021年9月10日的最大收益,这个最大收益怎么求?很显然,这是一个投资组合与时间序列的综合问题,需要基于整个数据进行分析与挖掘。
而幸运的是,问题所涉及的可选资产配置并不多,只有黄金和比特币两种产品。一般的如果碰上了多支股票进行配置那么还需要基于它们的统计特性进行一轮投资选股。对于这种时间序列+投资组合的问题,我们一般把它分解为“预测”+“优化”两步走。这个地方如果使用动态规划则需要谨慎,因为在这种投资组合问题下使用动态规划是无法预判未来发生的情况的,只有在开启上帝视角的投资问题中才可以使用动态规划,所以就我了解的情况而言,使用动态规划的同学普遍做的比较差。
就预测的部分来讲,这是个典型的数据驱动过程。数据驱动的背景之下,命题人想要考察的本质上还是学生对数据的敏感度和处理基本功。那么对于时间序列数据而言,这种面板数据的重要性要高于常规数据,因为面板数据中每一条样本它是有序的,是分了历史和未来的。
你永远不可能用未来信息推历史,因为你根本不会知道未来。而就时间序列的处理方法,仅仅是一个预测,也会有很多的一题多解的策略。那么就方法选择而言,不少同学可能会盲目的使用灰色系统这一新晋之秀,而忽略了这个问题是否满足灰色系统的条件和特征。时间序列预测的方法需要取决于数据的条目和平稳性,小体量数据可以用回归做长而粗的趋势预测,中体量数据可以用灰色系统做中而稳的趋势预测,大体量数据可以用神经网络或者ARIMA做短而精的精确预测。
这个问题中有五年数据,以日作为频率再考虑休盘也就是将近1600余条数据,体量算中大型数据,可以使用ARIMA系列。而不少同学问这个问题用神经网络可不可以预测呢,其实是可以的,但是神经网络的预测其实实验以后就知道并没有那么好。
就优化的部分来讲,优化模型是基于之前的预测结果进行。比如,如果投资者可以每日调仓(也就是每天都可以改变我的资产配置),那么很显然,模型只需要对明天的价格做预估就可以知道把钱投在谁身上才会赚(或者赶紧套现出来就不会亏很多)。这是短期预测的目的,盈利也就只需要算明天预计价格减去今天的购买价格就可以算出升值了多少。
那么投资的第一个思路有了,就是用预测代替上帝视角;而第二个思路是用什么来预测呢?马科维茨理论给了我们很好的解释:投资无非是两个要点,第一要利润大,第二要风险小,所以在投资之前就要先选择好发展潜力好的产品,投资的时候不要把鸡蛋都放在一个篮子里,套现以后只要赚到了钱就不用过分追责认为自己是不是少赚了钱。那么这个问题就被抽象为一个多目标优化问题,即:构造风险函数使其最小,同时构造收益函数使其最大,约束条件有三个:
第一,二者配置的权重不能超过100%也就是1000美元;
第二,比特币如果亏损不能亏光投在比特币里面的钱;
第三,黄金如果亏损不能亏光投在黄金里面的钱。
条件二和条件三也就保证了即使亏损我不能亏损过本金。可以这么构造模型:
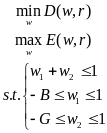
D也就是风险,可以用组合投资的方差表示;E为收益,可以用组合投资的数学期望表示。但是注意一个问题,这里我的投资收益是扣除了手续费的,所以计算并不是简单的数学期望,而是:
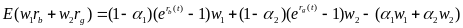
D的表达式同样可以写:
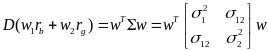
这个问题是一个多目标优化问题,那么解决这种问题完全可以再引入权重系数综合E和D构造新的目标函数求极值。
第二问需要验证问题一的策略是否正确可行,其实可以旁敲侧击,用其他的优化方案来证明“ARIMA+马科维兹”的配置是最优即可。
关于预测的准确性问题在问题一中已经通过实验可以对比,而关于优化的方案笔者还可以提供两个好的方案:第一个是最大夏普比率,这一方法的思想其实与马科维兹有着异曲同工之妙,但是在对E函数和D函数的综合上使用夏普比率进行融合:
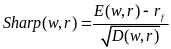
其中RF是无风险利率,按照美联储标准取0.04即可。第二种是风险平价模型,这一类模型则考察的对象是使得投资后黄金的风险和比特币的风险等价化,模型形如:
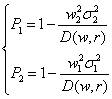
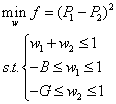
通过对不同模型的比较可以完成灵敏性和正确性的分析。
查找资料和数据的网站推荐
美国统计局:http://www.census.gov/
美国农业部数据:https://www.usda.gov/topics/data
世界卫生组织数据:https://www.who.int/data/gho
美国政府网站:https://www.usa.gov/
美国劳工部劳动统计局:http://www.bls.gov/
美国商务部:https://www.commerce.gov/
美国国际贸易协会:http://www.usitc.gov/
美国交通统计局:http://www.bts.gov/
美国国家统计局:http://www.fedstats.gov/
部分情况下,真实数据不易找到,可以尝试以下两个解决办法:
第一,如果这道题并没有限定国家,可以考虑以中国作为研究对象,找自己国家的数据还是相对较为简单。
第二,利用数据挖掘的能力,需要一定的技术手段去收集数据,比如爬虫技术,自己去爬一些可能用得到的内容。或者可以去一些数据科学竞赛平台上去找一些现成可用的数据集,如:
天池大数据数据集:https://tianchi.aliyun.com/dataset/?spm=5176.12281905.0.0.358b5699IjonJQ
UCI机器学习数据库:https://archive.ics.uci.edu/ml/index.php











