2022年CTST第一轮测试(一)试题及解答
这两周进行了集训队一阶段考试，尽管笔者太菜没资格参加，但也在第一时间做了考题，现在本文将给出第一次测试的解答，至于第二次的解答，应该也会在这两天尽快更新。
在解答中，笔者做出来的题目，大多写有思路分析和批注，给出的基本是自己的原始解法，和标答及其他解法或许是大同小异，部分解答也会据此优化改良。其余的题目这里便只放出标准答案。鉴于笔者水平有限，不当之处还望读者海涵并不吝赐教！（大佬可以直接关闭页面了）
1、试题
2022年CTST第一轮 测试(一)
以下即将进入解答部分
2、解答
2022年CTST第一轮 测试(一)
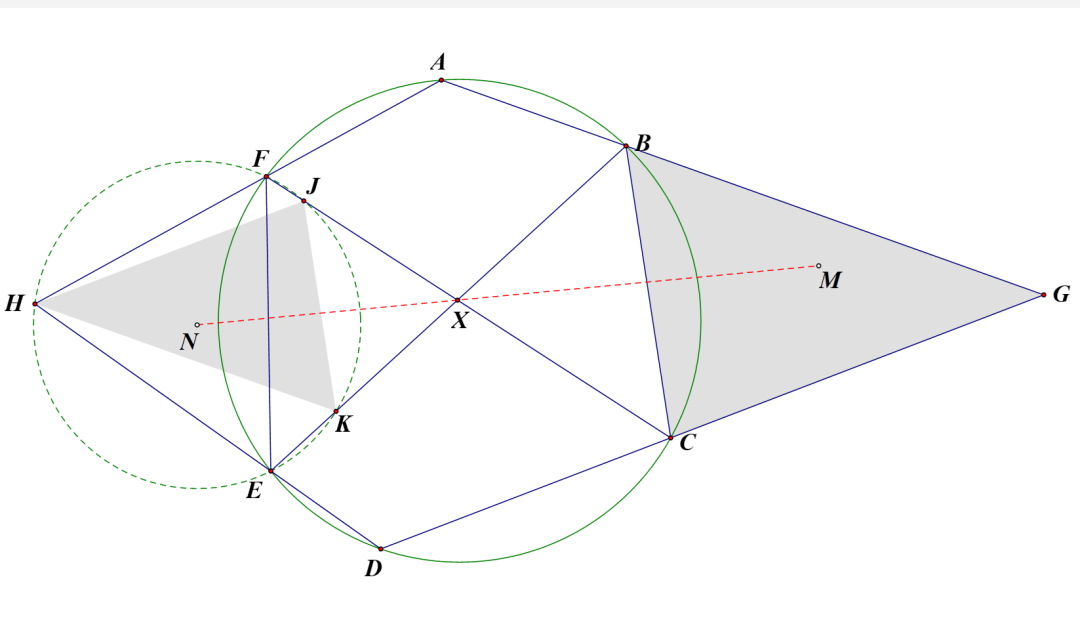
分析：此题过于简单，甚至是一道在网上出现过的陈题，圆内接六边形一出现，条件反射式地反馈出Pascal定理，而后不难发现平行，计算比例线段即可. 另有一个纯导角的位似证法，本质上就是照抄了一下Pascal的纯几何证明，详见图二.
解答：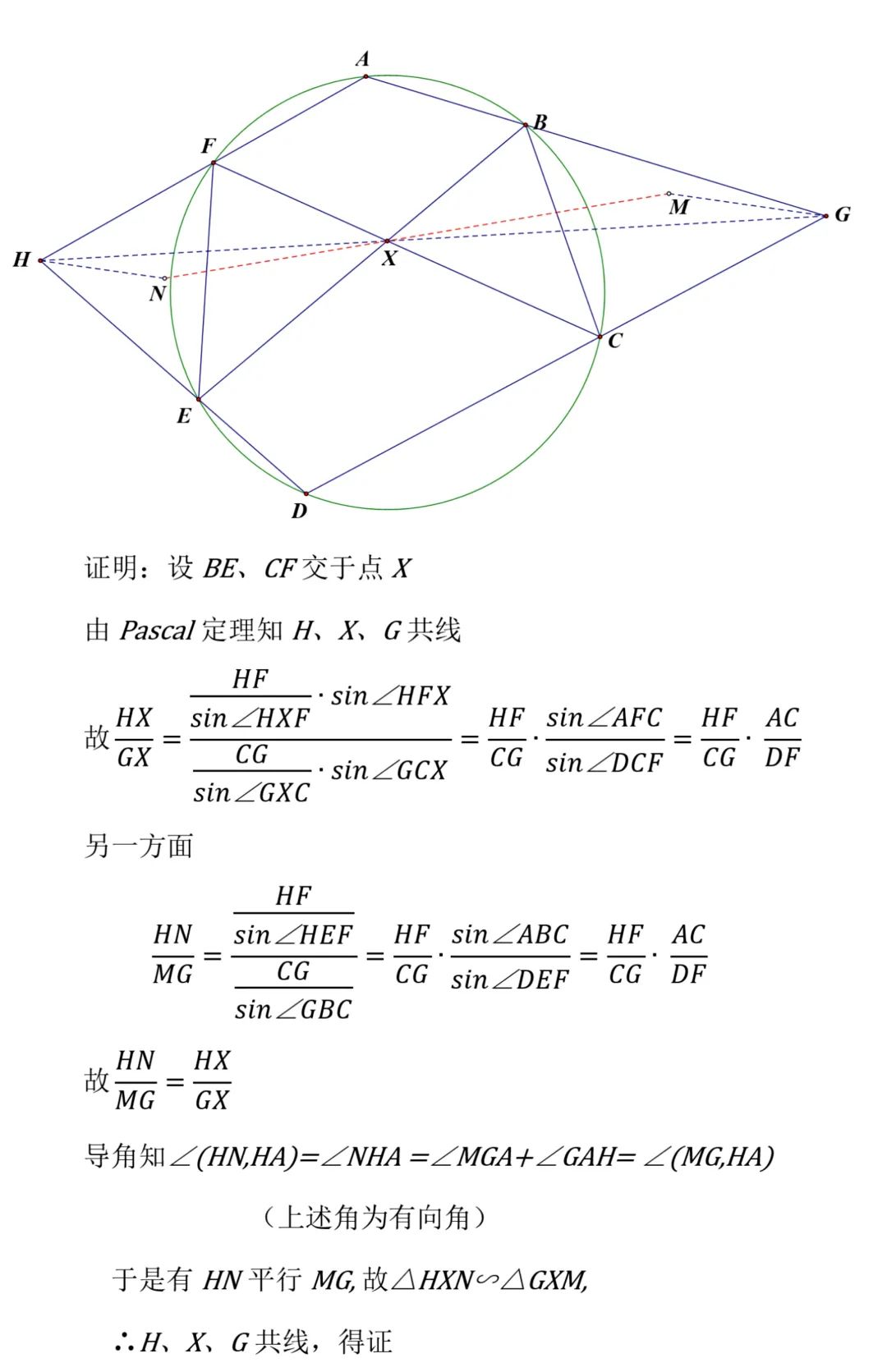
位似证法：
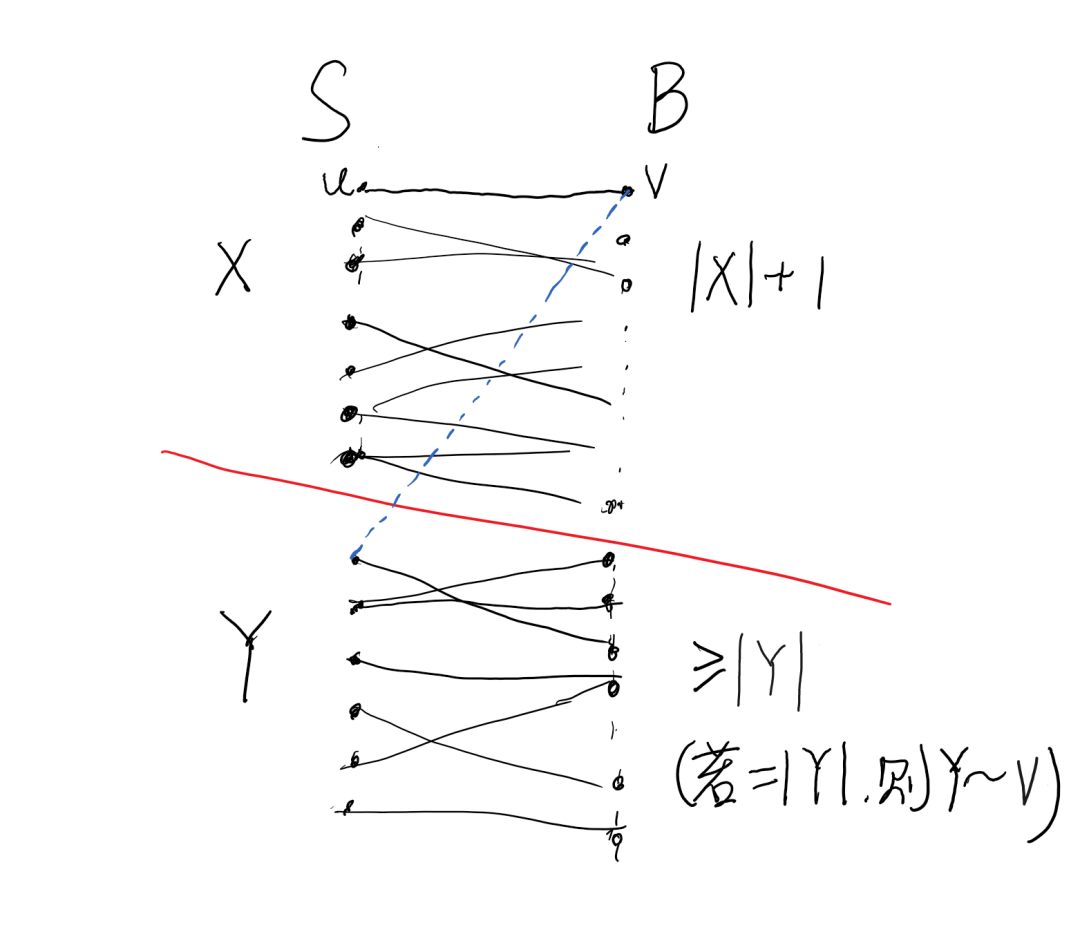
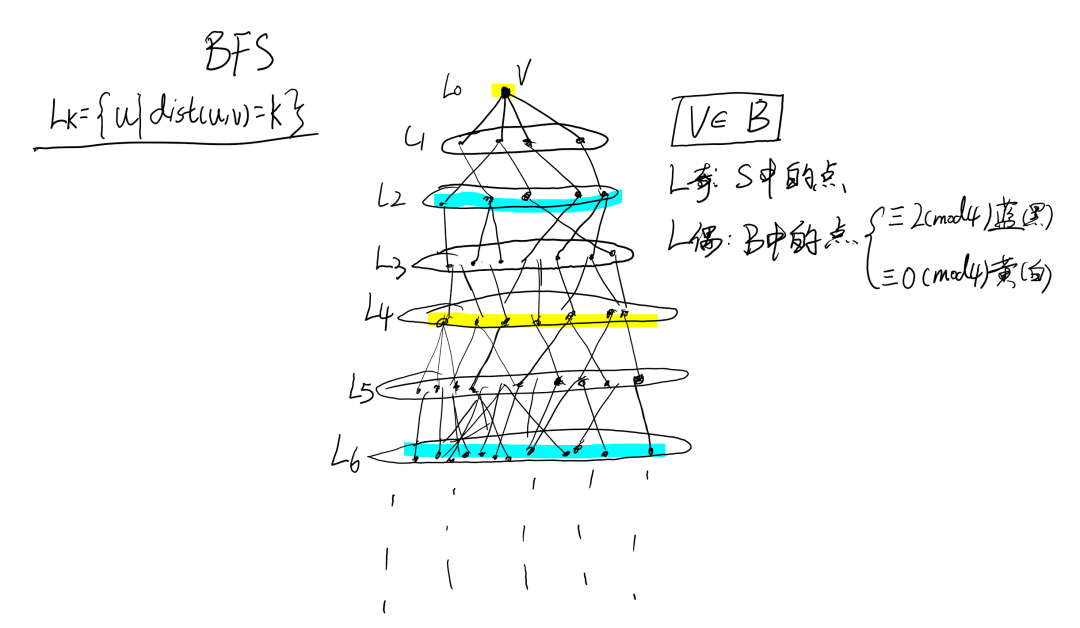
分析：在某个任给的无穷集中讨论数论问题，常用的一个性质是：模任意一个正整数，都必有其某个剩余类在集合中出现无穷多次，在本问题中亦用到这一性质. 首先的一个自然想法是：如果能挑出子集B，使得B 中任意P个数的和都不是p 的倍数就好了，这样取完算数平均值直接就不是整数了，自然不在A 中.有了这个想法，我们再结合开始提到的性质，会发现如果模p的剩余类中有两个都在A中出现无穷多次，就可以解决问题. 而后讨论只有一个类出现无穷多次的情形，用带余除法表示后，其实可不妨同时减掉余数，再除以p 考虑，而这就相当于模p² , 于是想要在反证的假设下，归纳证明模任意p 的幂都只有一个剩余类出现无穷多次，而后根据这一断言进行构造和说理即可. 此题没有本质难度，但说理略有些繁琐，部分过程可以优化(比如将前面提到的归纳法改成反证法，取最小的反例导出矛盾)，这样便可缩短证明长度.
证明：假设结论不成立，也即不存在这样的集合.
我们可先不妨假设 中有无穷多个正整数，否则全部取相反数即可. 且我们删去 中所有的负数，将其变为正整数集，证明此时仍然可举出反例，进而导出矛盾.
一道屠场题，貌似没听说有人在考场上做出来. 赋权得到界是自然的，而后的证明则是极为困难. 由于笔者能力有限，这里就不做解释了，直接贴标答吧.
第一个难点大概在于作出标准图，这里先给出一个标准图作法.
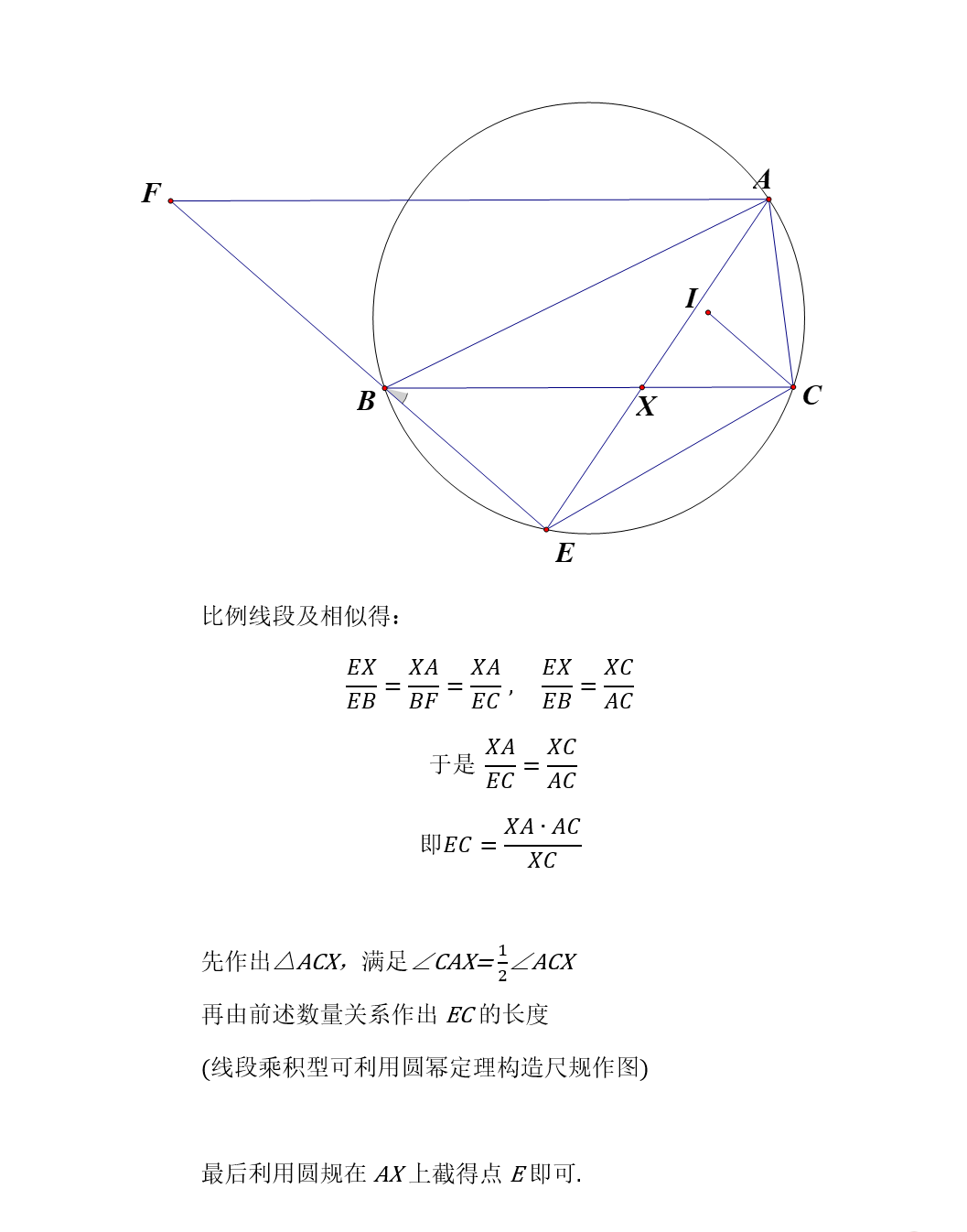
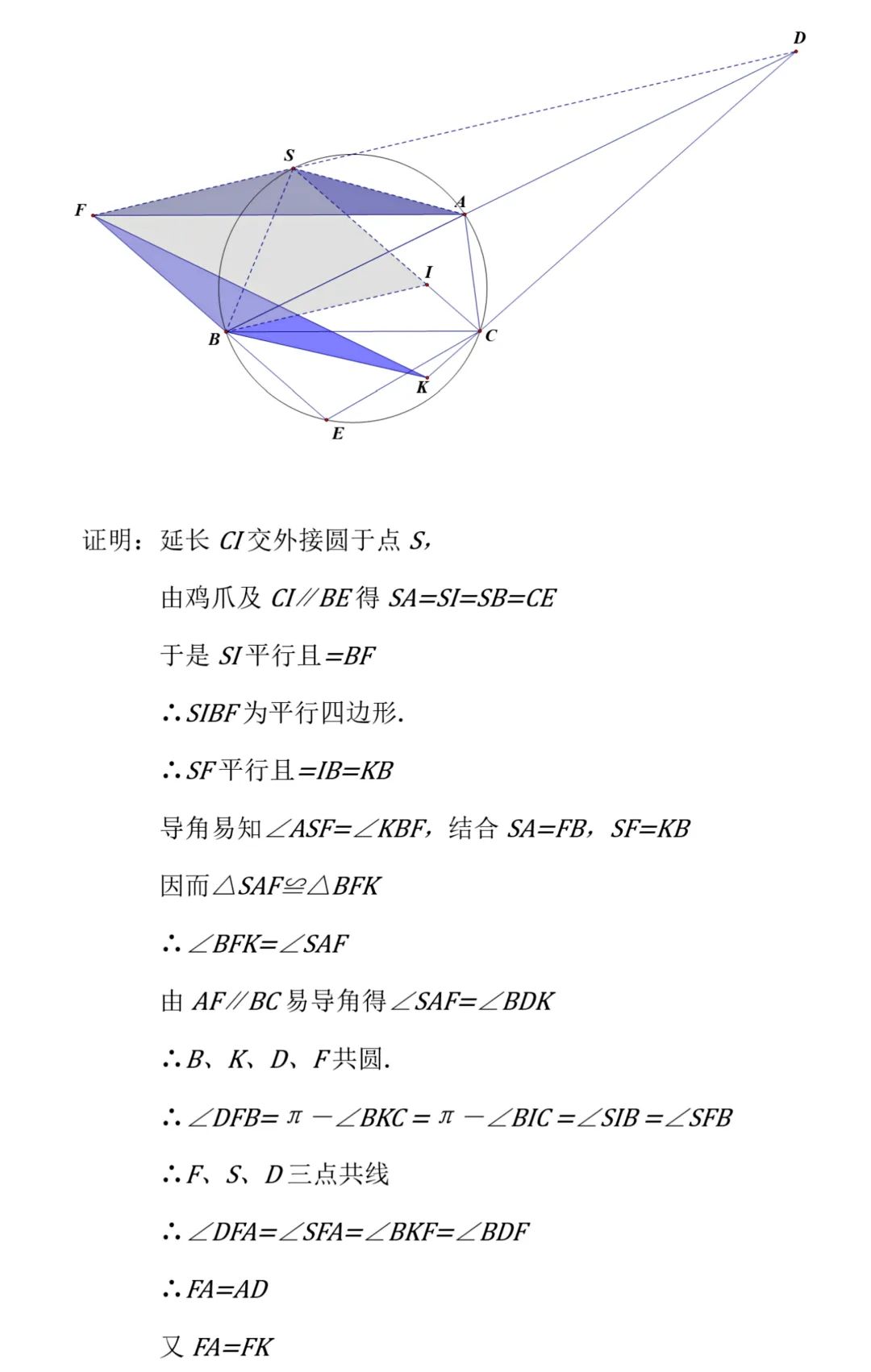
其实添出弧AB中点S还算是比较自然的，不过笔者一开始确实没有想到，而是根据边相等的条件先取出了弧BAC中点M，绕了一圈才回来. 思考过程如下:
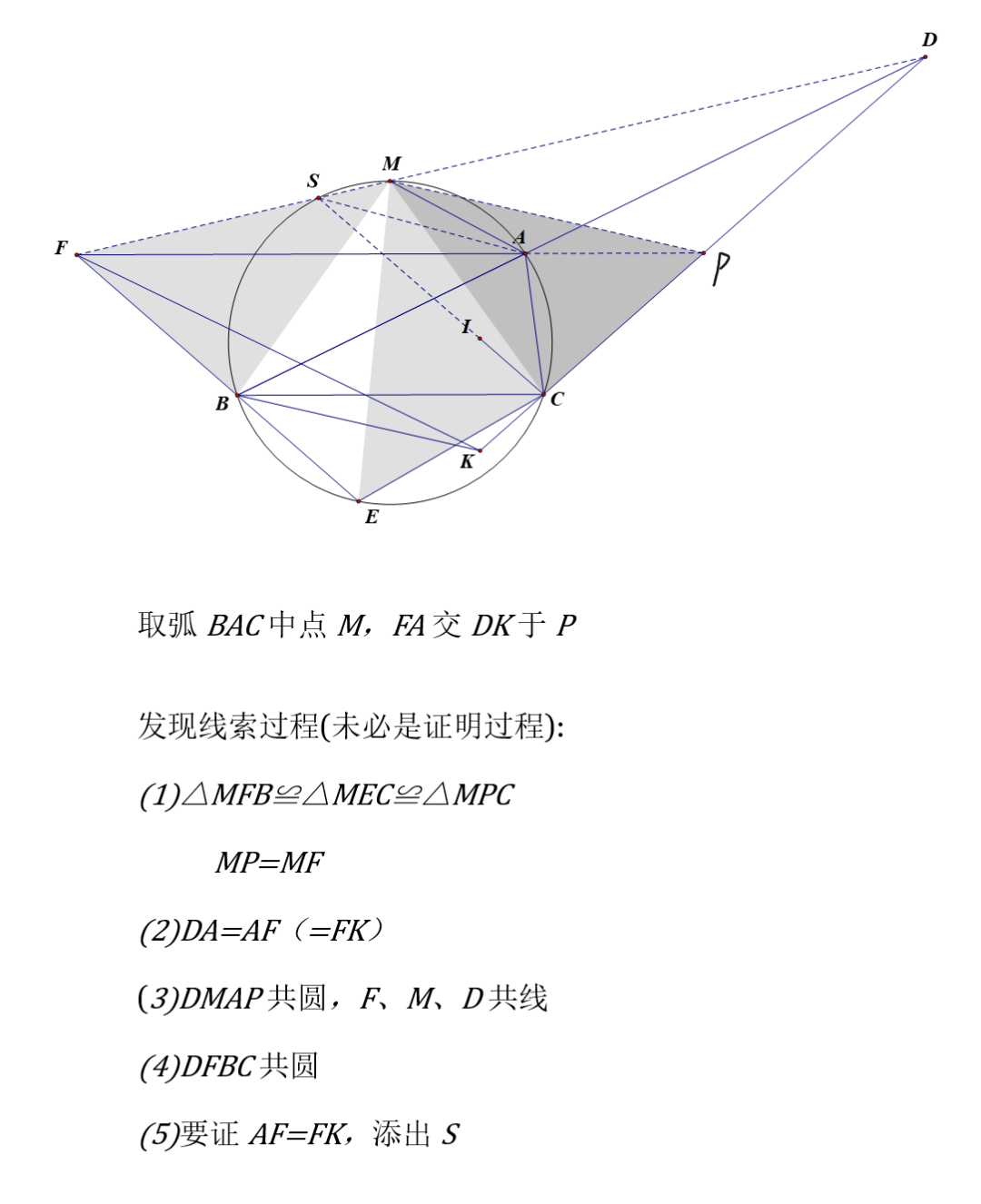
图中提到的性质，读者自证不难.
可以先取出满足取到最大值的一组复数，然后根据最大性刻画取等，再回过头来计算最值，最后也能得到答案，不过感觉不算很严谨，也懒得写了，这里还是给出标答
【竞赛报名/项目咨询+微信：mollywei007】
