递推方法解决AMC组合数学或概率论问题

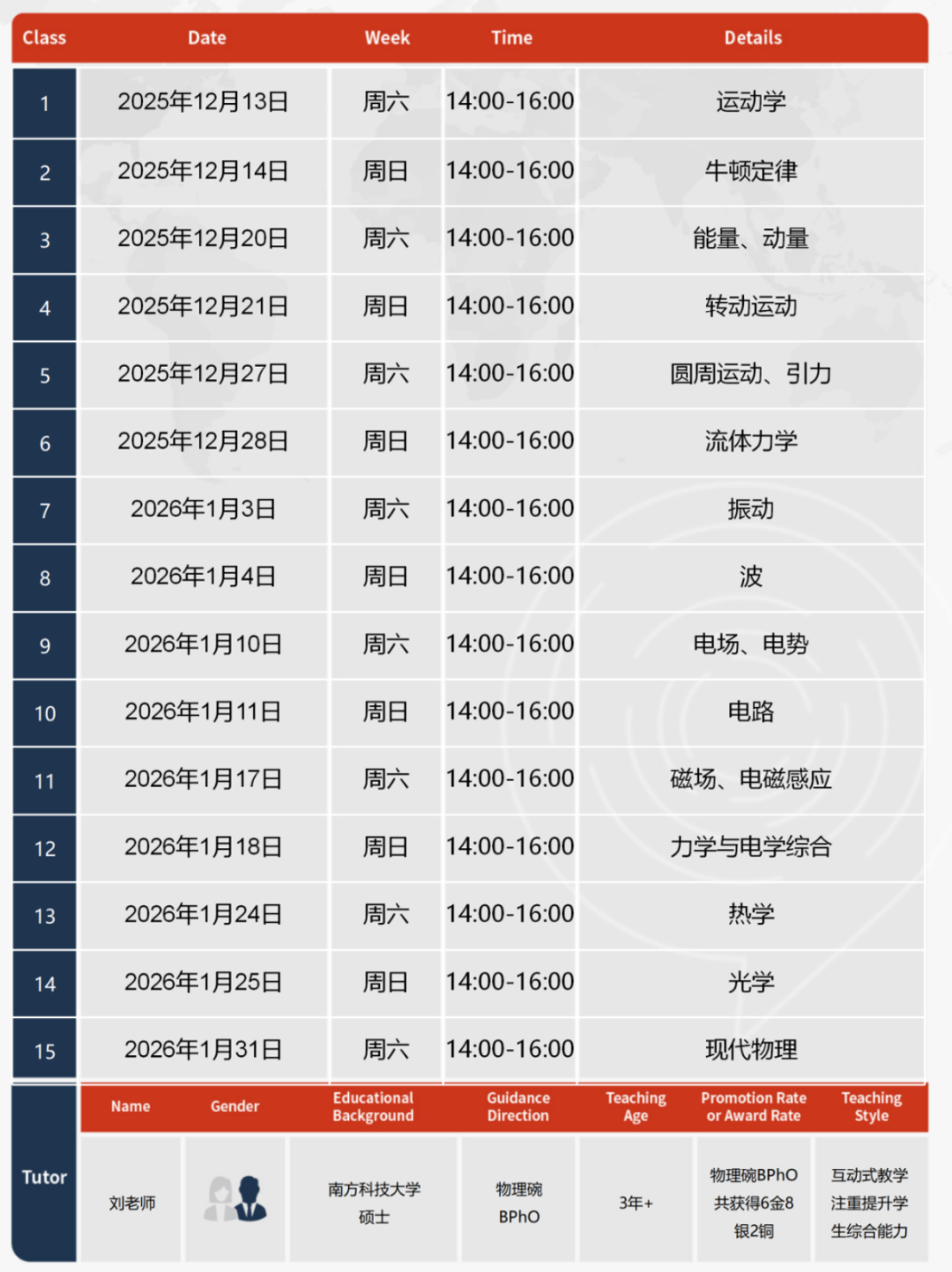
在2014 AMC10B的25题中，AMC10首次出现了必须使用递推方法来解决的组合数学或概率论问题。

鉴于在MAA的众多竞赛中，递推数列的通项公式求法（例如特征方程、不动点法、母函数（Generating Function）等）通常是不要求的（总是可以找到不依赖于这些方法的题解），于是这类问题的难点会全部拥挤在列出递推式这部分，数字本身都是容易计算的。

我们首先看一下这个题目，大家就会直观地认识这类问题的风格：

容易看到，本题的难点在于它并没有规定Frog逃出水池的跳跃次数，并且与随机游动（Random Walk）类似，它在每个pad上都有个事先规定的概率向左或向右跳跃。

因此，2个直观的感受是：

➜ 也许此Frog会在这些pad上不断左右来回跳以至于既没有被吃掉也没有逃出去；

➜ Frog的跳跃具有很强的“向心力”，即它向Pad 5跳跃的概率随与Pad 5的距离增大而线性增加。当然，题目数据给的是非常小的，一共只有11 pads。

（Random Walk in 1-dimension的实例）

在事件包含的样本点是无穷多个的时候，由于缺乏Lebesgue测度和极限等工具，中学生通常难以理解这些问题中的“概率”是指什么，或者如何计算，可以说这是AMC对于中学生抽象思维和解题技巧提出的较高要求。

单纯从解决问题的方法上来说，这类问题常常需要一些“对称化的思想”辅助。

首先我们列出所有pad上面的向左、向右跳跃概率：

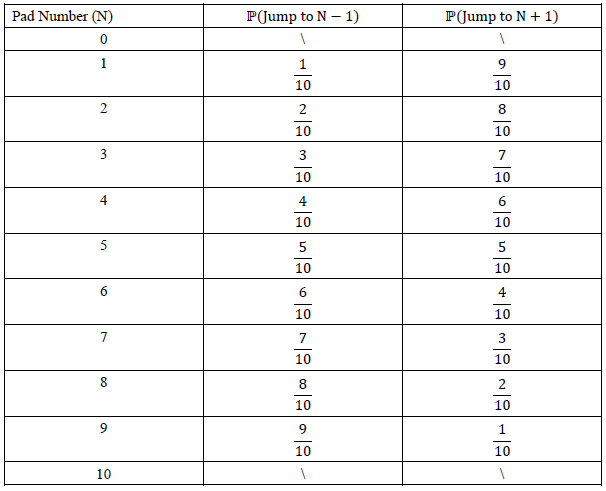
此类递推的本质，是在求含有无限样本点的事件概率时，利用递推化为方程求解，绕过了复杂的分步概率和级数求和。

不论如何，本题都算是一个较难在考场上完成的试题，事实上递推求组合问题在AIME当中也比较常见，比如13届AIME当中就有类似的例子，只不过即使在AIME中，递推的方程组数也不会超过三个。

Solution：

我们使用递推的思想完成本题。

当然，递推方法也可以用于求复杂的序列计数题。比如第26届AIME的试题：

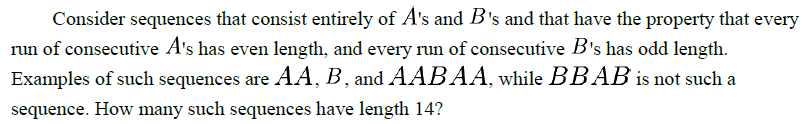
（本题建议读者先自行列出递推式，再看我们的解答）

Solution：