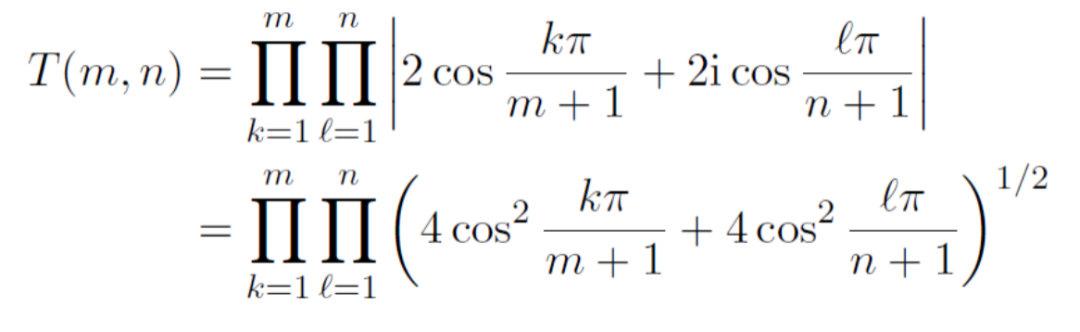矩形棋盘的多米诺覆盖方法数
Number of Domino Tiling in Rectangular Chessboard
鉴于笔者水平有限,一些严格的图论语言无法翻译成中文,所以本文中一些定义和语言我们沿用2021年由剑桥大学出版的组合数学教材叙述方式。文中所有定理和引理读者都可在阅读时先尝试自行证明,再看文中的证明,分析两者的区别。本文中的情形适合初学者,而一般情形适合有一定代数、图论基础的读者,总体而言我们的文章基于Kasteleyn教授和Carnegie Mellon University 的 Brendan W. Sulliva教授的工作(感谢!)。
下面,让我们开始吧!
首先,我们简单地给一些定义,考虑一个的矩形棋盘和若干可任意旋转翻折的多米诺骨牌:
Definition
![]()
Example
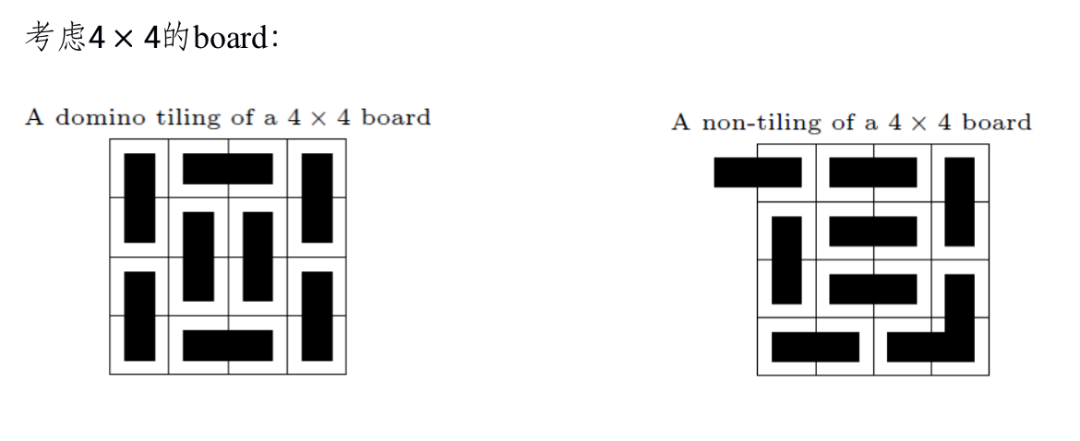

Fact
![]()
Proof
![]()
Example
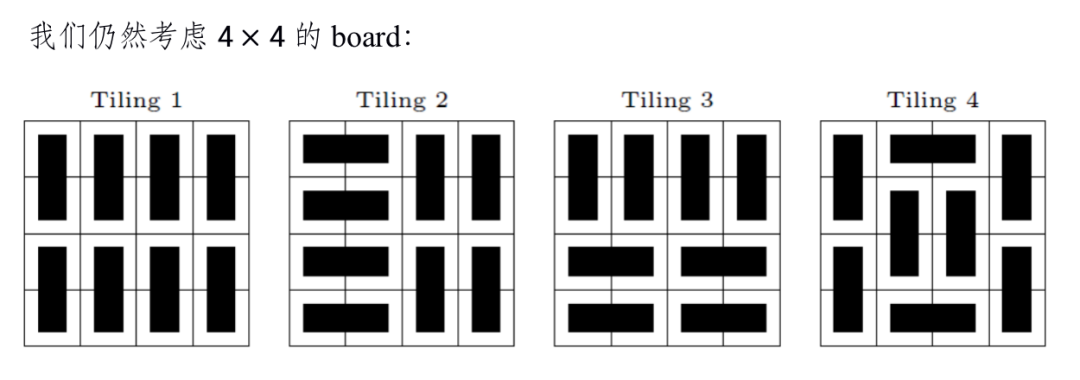



Special Case: How many ways can one cover a 3 x n chessboard with dominoes?
Solution
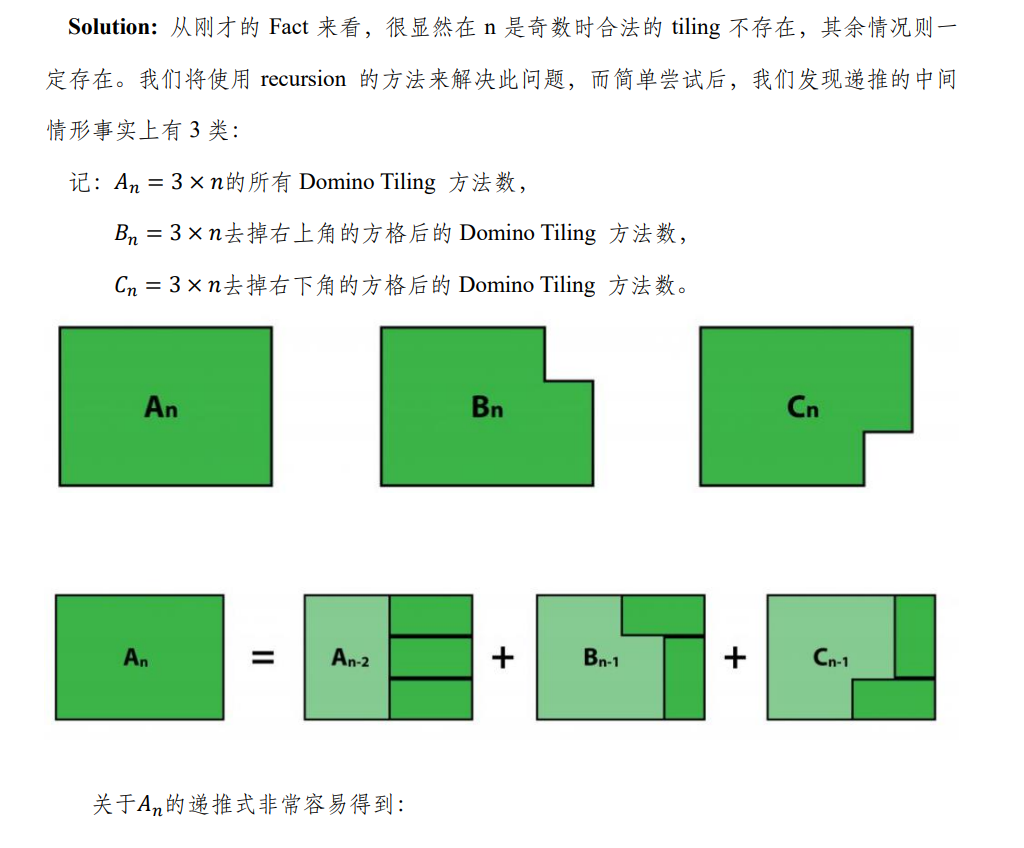
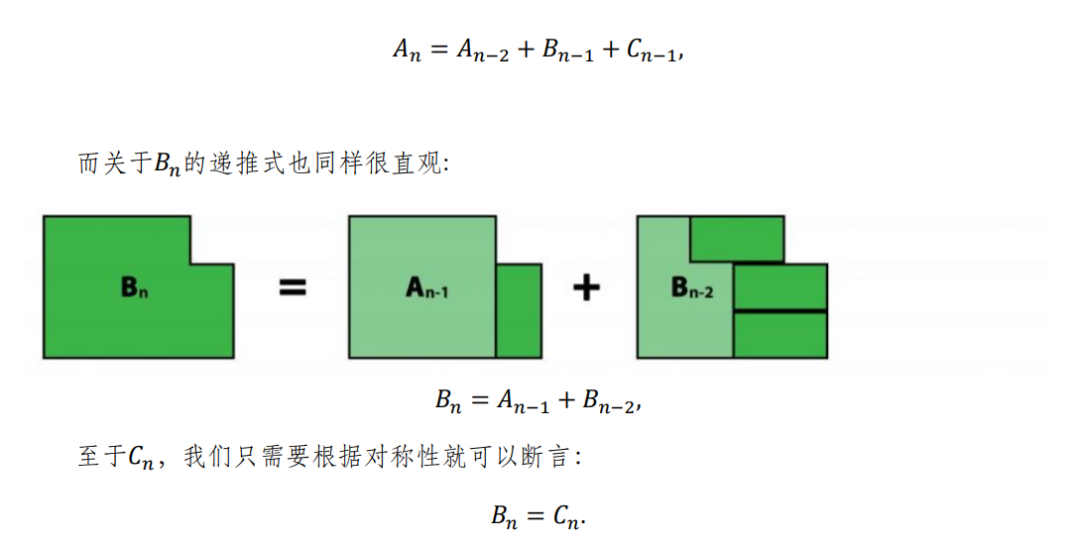

到此,一个自然的问题是,我们能否把这样的方法推广到一般的chessboard上。
事实上,如果记chessboard的Tiling 方法数,只要命m=4就容易发现,T(4,4) 的递推是个非常难以计算的式子:
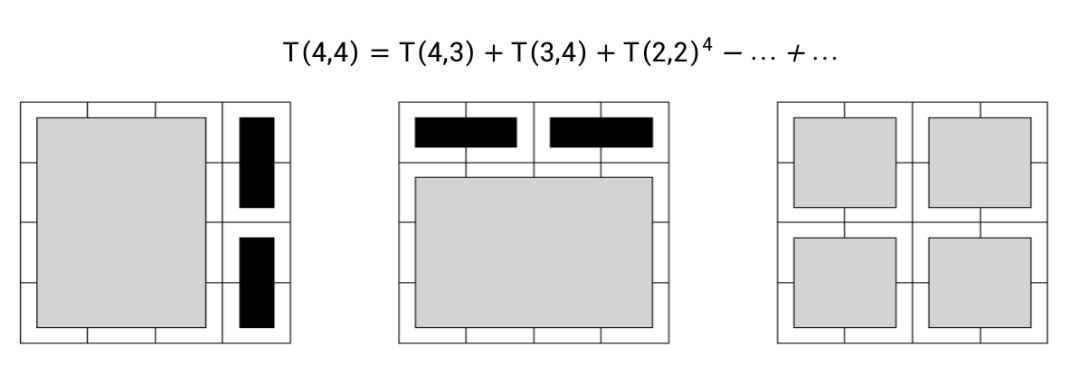
尽管许多数学问题都可以用类推的思想,但很遗憾的是,Domino Tiling并不属于此类,因此我们要使用图论的方法得到其一般情况的解答。这个问题最早是由 Temperley & Fisher (1961) 和 Kasteleyn (1961) 分别独立解决的,这几位数学家都对于图论做出了很多贡献。
下面,我们将要使用图论技术,将这个问题首先抽象为一个平面图,再利用邻接矩阵(adjacency matrix)把它完全转为高等代数问题。此方法最基础的思想是:一个Domino Tiling 唯一对应一个chessboard 的underlying grid graph 的perfect matching。换句话说:只要确定哪些方块是被同一块骨牌覆盖的,也就确定了一个Domino Tiling,这意味着我们只要“恰当地”归类chessboard上的所有方块使得这样的归类方法的确是个tiling。
我们以一个具体的例子来阐述图论抽象操作是如何完成的:
STEPI:
把一个chessboard中的每个小方块抽象为一个顶点(vertex),如果两个小方块相邻(也即他们至少有一条公共边),则在它们之间连一条边(edge),这样的结果我们称为一个underlying grid graph:
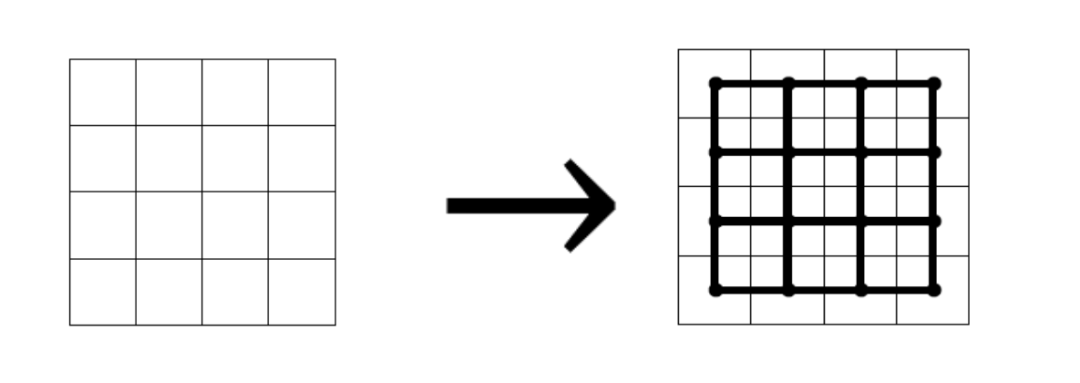
STEPII:
我们把一个Domino Tiling看成是对于underlying grid graph中的edge的一种选取,目标是要覆盖顶点集(vertex set):
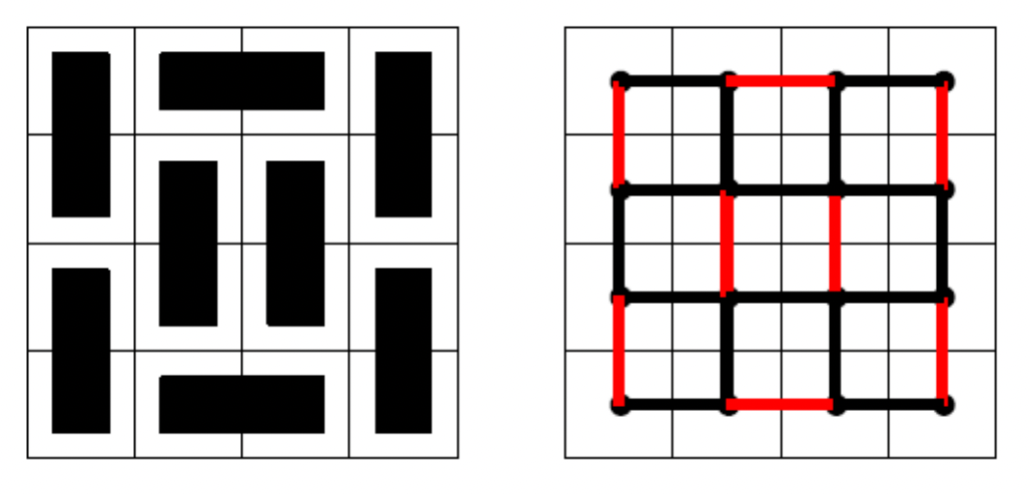
用图论术语来说,这就是个perfect matching。
Definition

Example

Note

Fact
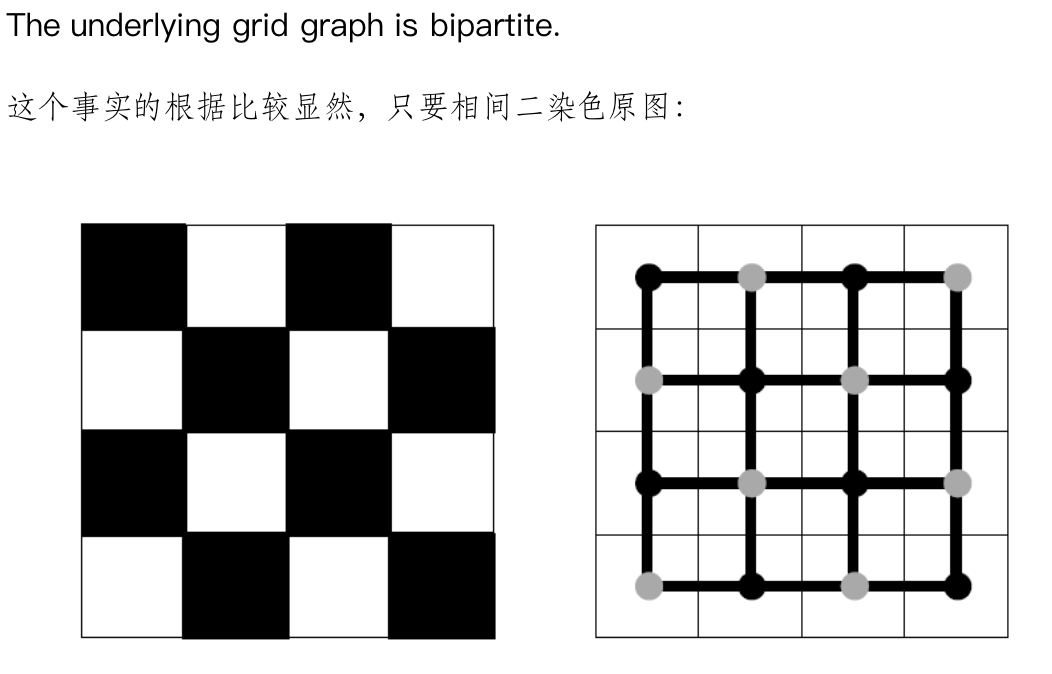
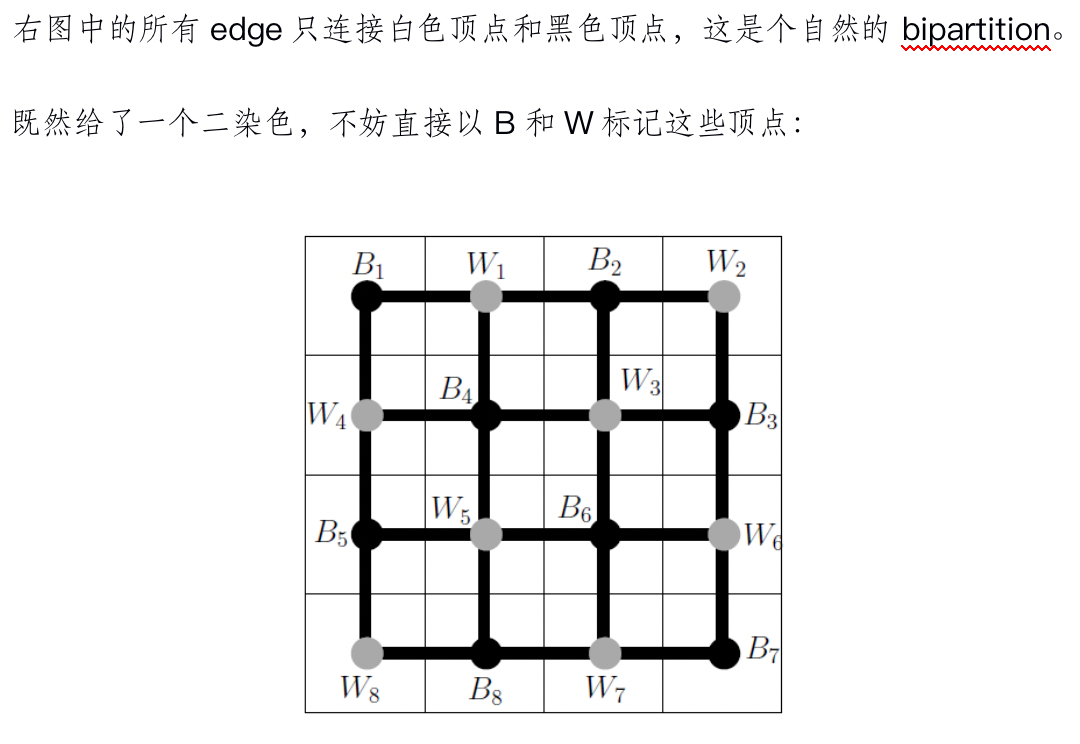
Note

Definition
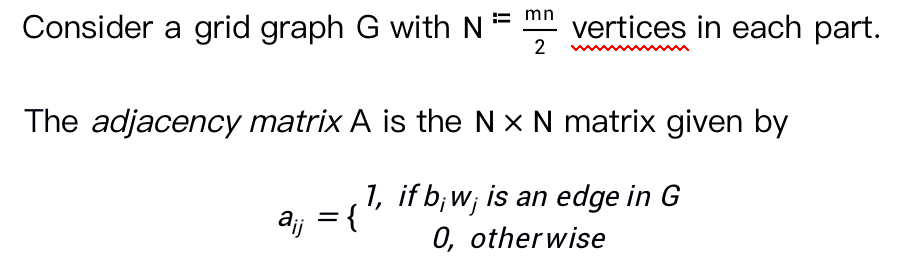
Example
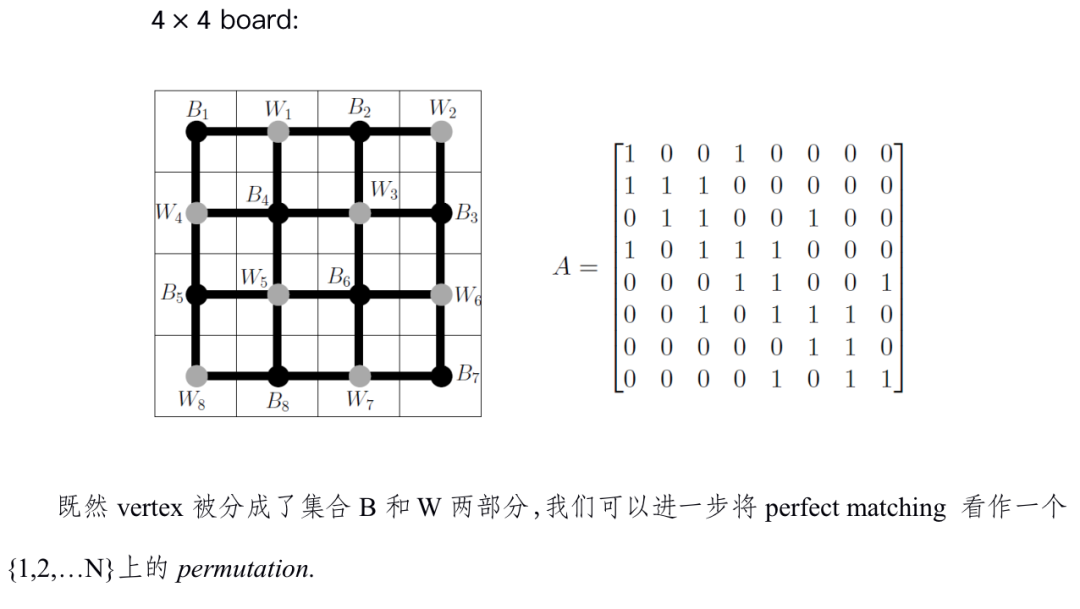
Example

Example
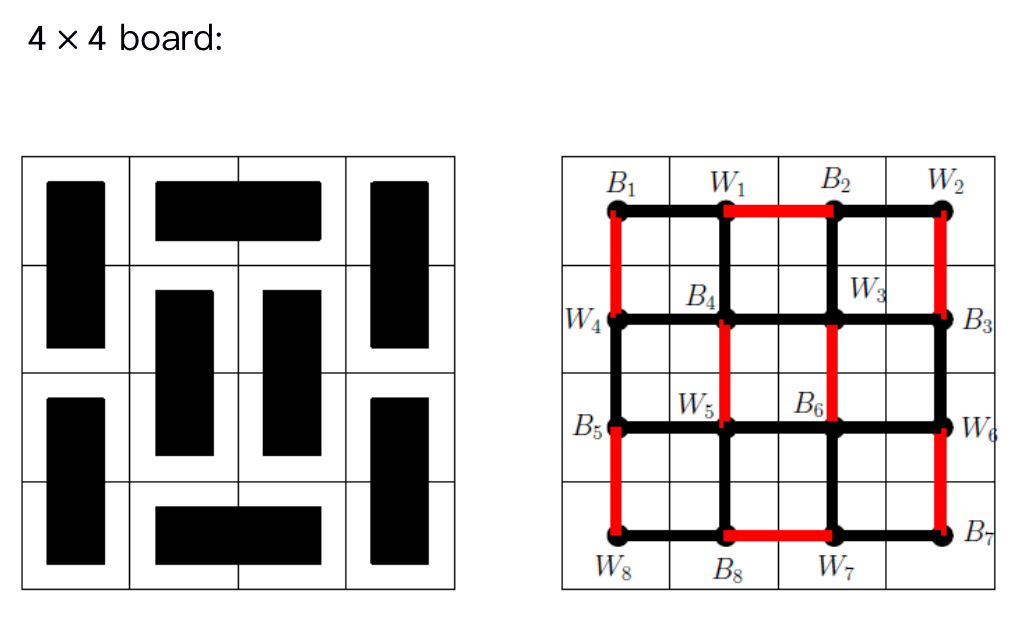
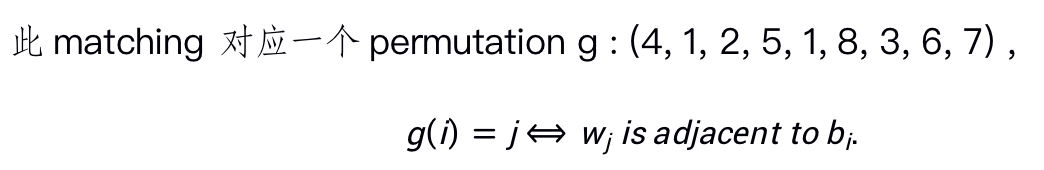
Note


Definition

这个处理的方法,我们称之为signing:
Definition

Example
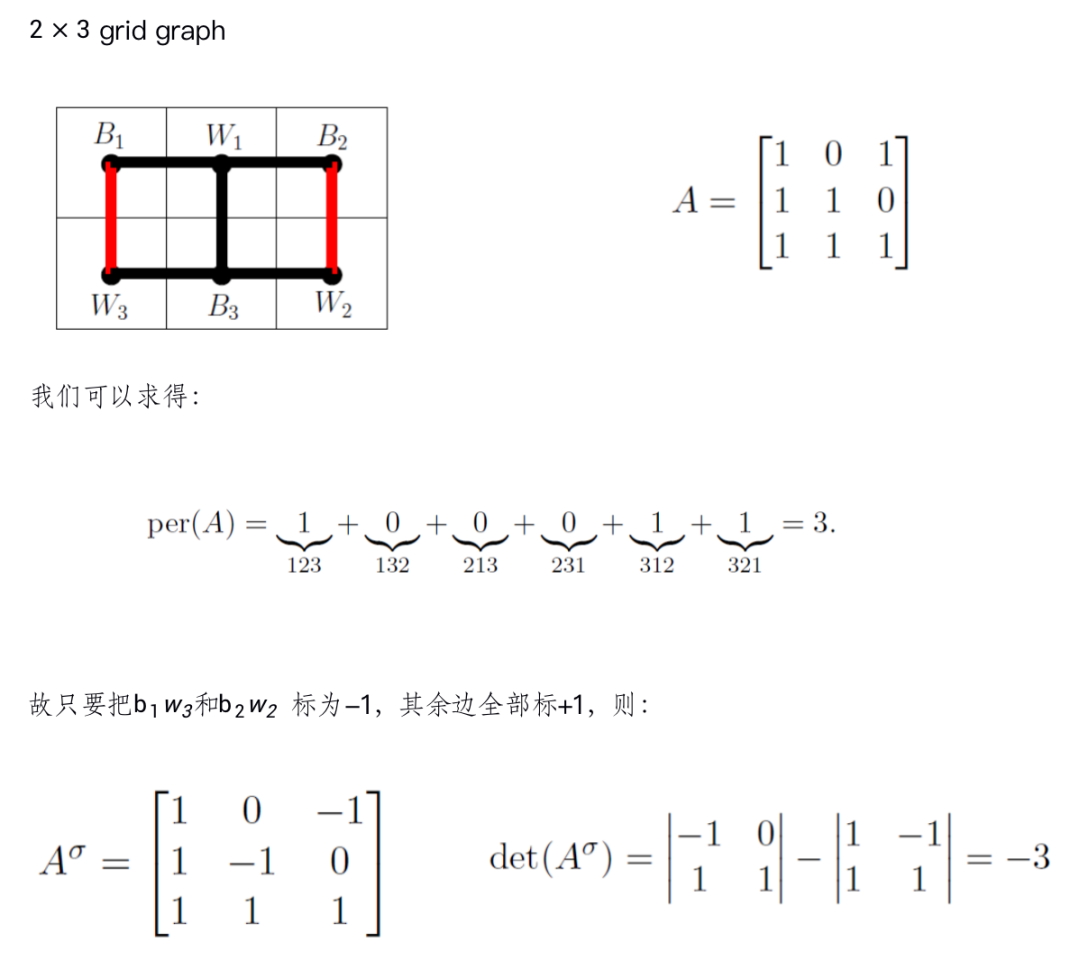
下面,我们将要证明一个定理,先给一个不太严格的叙述:
Theorem

Definition

Definition
![]()
Definition
![]()
Definition

我们的grid graph 是2-connected的,可以不严格地由下图示意:
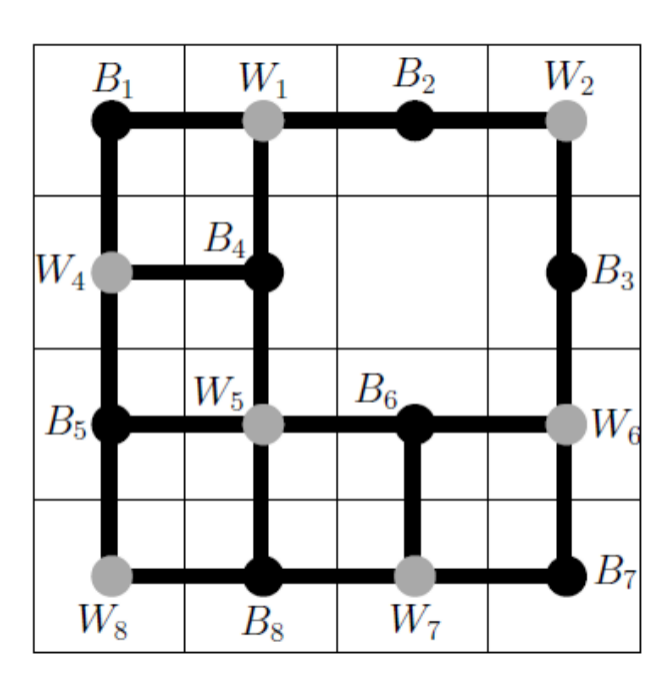
这个定理的叙述,现在可以很严格了:
Theorem

Note
![]()
Corollary

Definition

Example
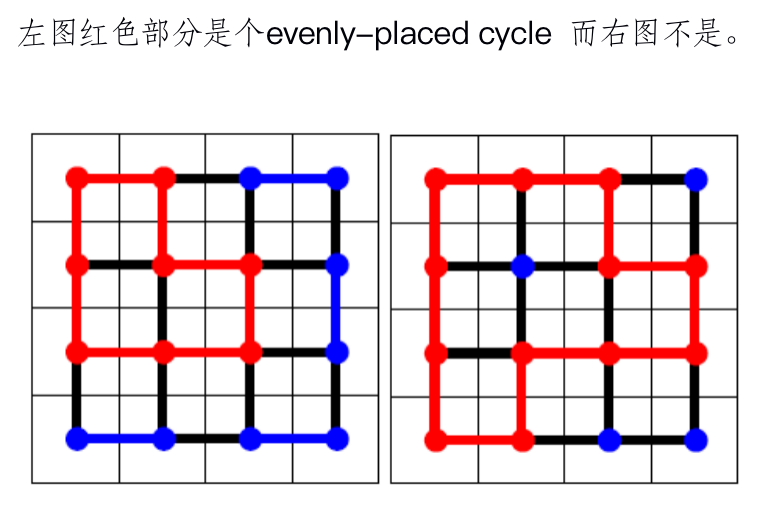
Definition
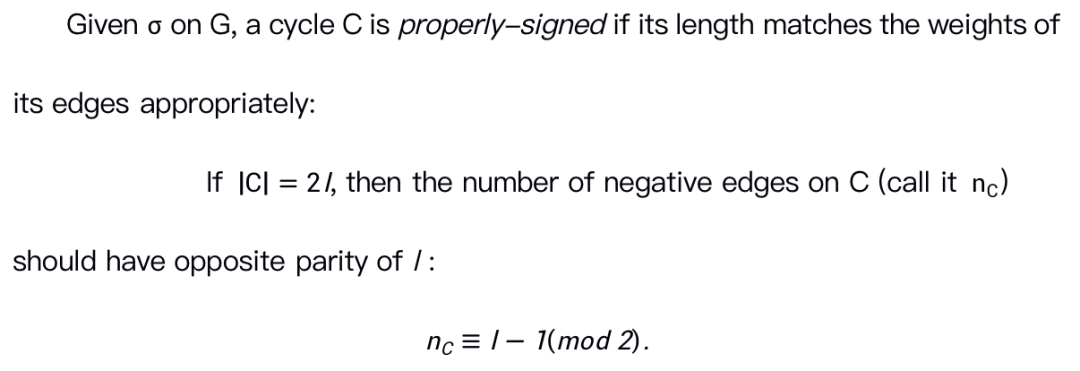
Example
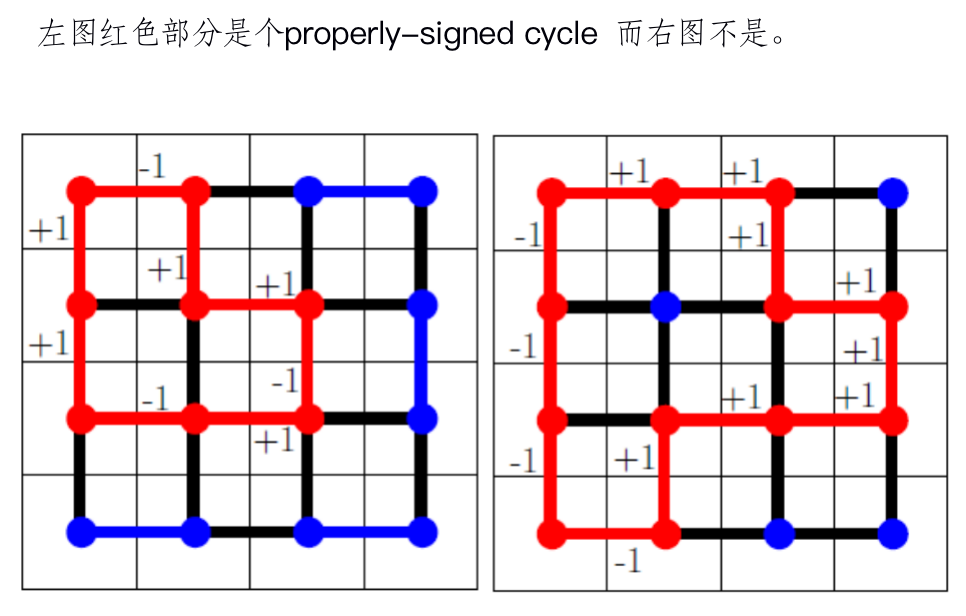
这样,我们就可以给出Lemma1了:
Lemma1

Proof Strategy

Proof


为此,我们先证明如下claim:
Claim
![]()
Proof

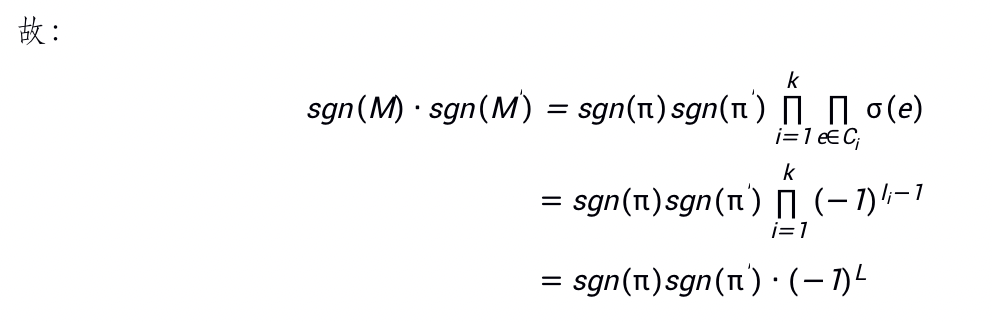


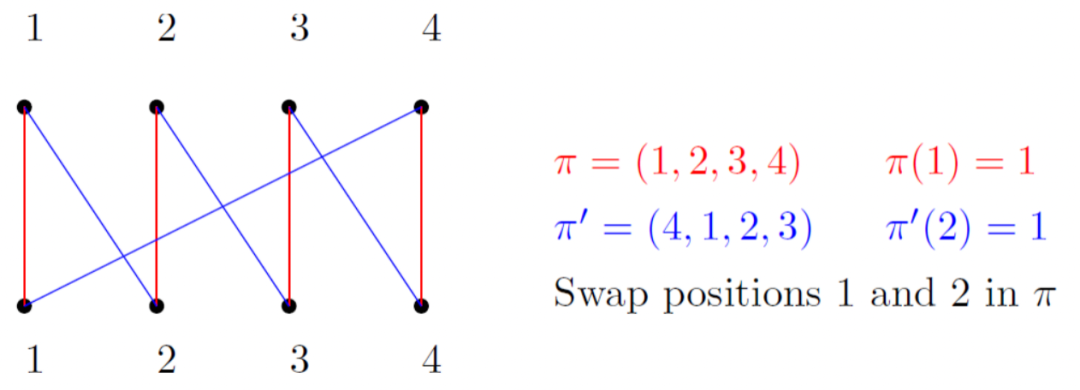
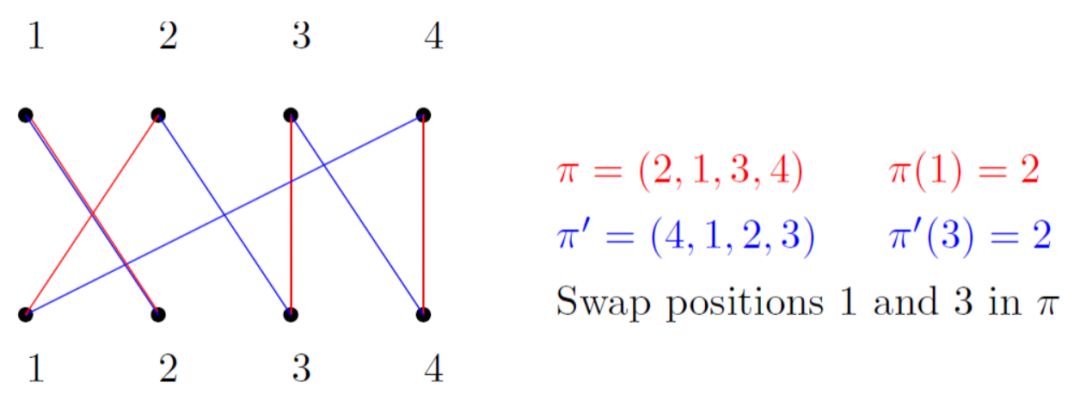
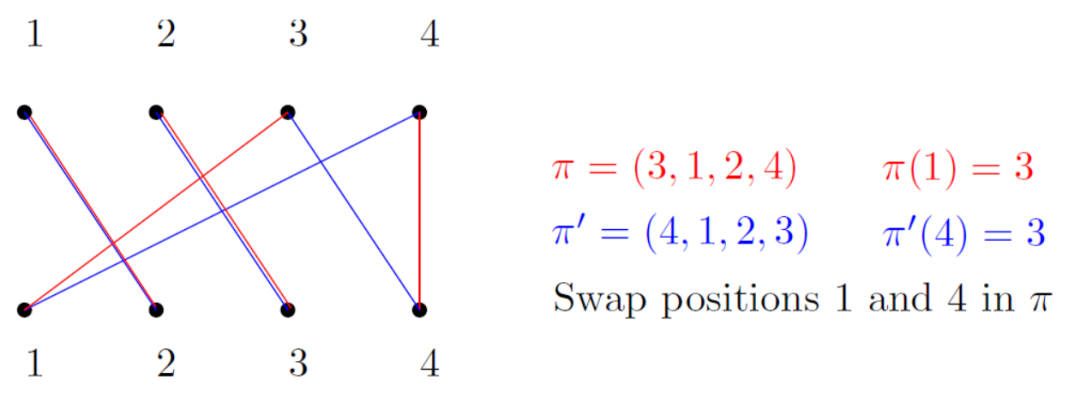
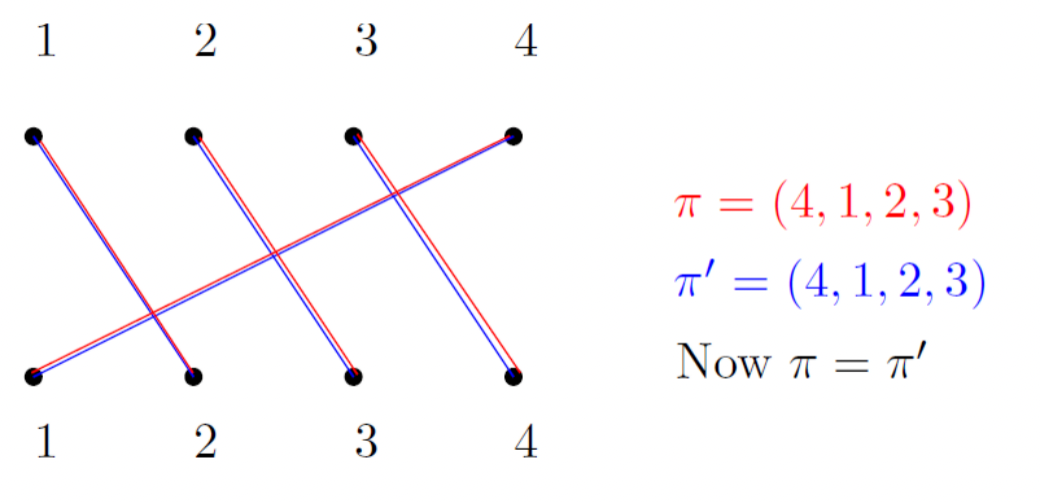
Lemma1从而得证。
关于第二个引理,我们将引入平面图(planar graph)中很重要的概念和定理,但篇幅有限,我们将不严格地介绍:
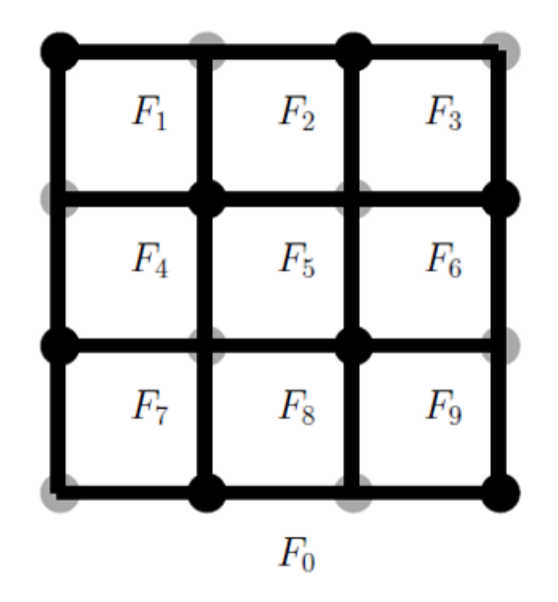
平面图的planar drawing就是一个把它画在平面的方法,每个固定的画法都会有vertex, edge,和faces(面),如右图有9个inner faces和一个outer faces。关于这些数量,Euler有一个著名的定理:
![]()
有了这些准备工作,我们来介绍Lemma2。
Lemma2

Proof


立刻可知C也是properly-signed,由Lemma1知结论成立!
经历了很长的引理和定理证明,也仅仅得到了T(m,n)的计算是多项式时间内的,真正得到它的公式还需要一些别的技术,这不是我们的重点。最后,让我们来看一下T(m,n)的形式: