在本月的每月一讲栏目中,我们将以一个新的视角,从所谓的 Fibonacci(斐波那契)数列开始,明确线性递推数列的通项公式的求法,以及高观点下的特征方程、特征值的意义。以下所有值均在复数范围内讨论。
(p.s.矩阵部分内容阅读与理解有困难的同学可以跳过Part2进入后面的内容~)
01·Fibonacci数列
首先,Fibonacci数列是一列不断增加的正整数列,满足
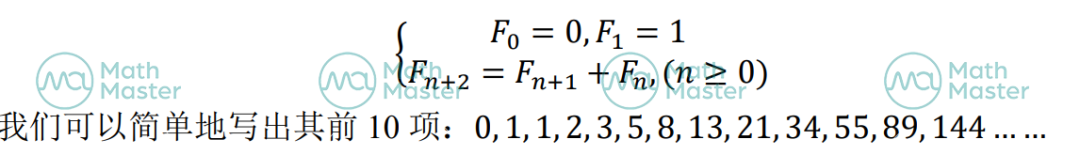
Fibonacci列具有丰富的性质,它有一些重要的identities如,d'Ocagne's Identity:
![]()
在数论和组合学中的树结构、生成函数等方面它也有一些应用。
Fibonacci列的通项公式求法在数学上被称为特征方程法,而此方程在多数教科书中总是不加解释地使用:

由此方法得到的通项公式虽然正确(可以由Induction证明),但很难给高中生合理的解释:为什么要用此特征方程、特征根?又是怎样想到这样的名词和方法呢?
下面,我们先给出k-阶线性递推的定义和通项求法,再进一步解释此方法。
02·k-阶线性递推
首先我们给出k-阶线性递推的定义和通项求法:

证明:我们从矩阵的角度来看特征方程

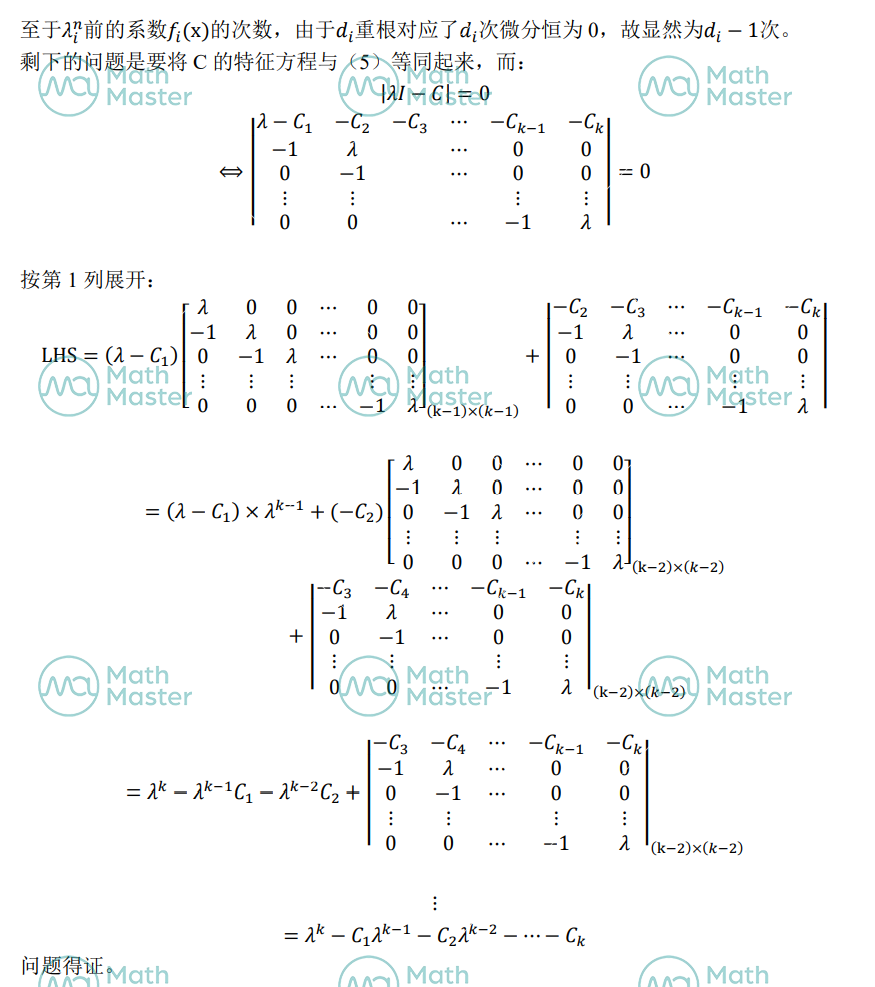
上述的做法对不熟悉矩阵的读者极不友好,故我们再从更高更抽象但代数上更简单的角度回看 Fibonacci 数列,由此来更深入地理解 k-阶线性递推。
首先对于 Fibonacci 数列,我们要回一个很杠精的问题:
![]()
想回答这个问题,需要你对数列改变一些约定俗成的看法。数列虽然长得像一列数,但它本 质上妥妥地是个函数。
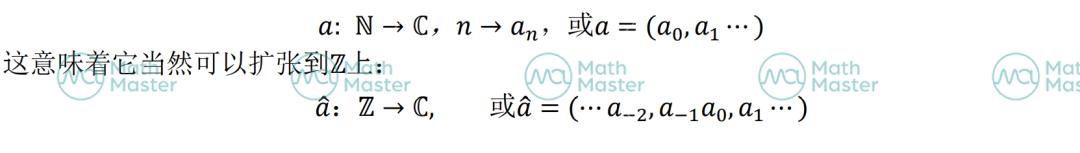

03·谱分解
说到这儿,一个合格的数学学习逻辑就是去研究解析延拓了,但我们决定就此打住,来看更有技术含量的内容:谱分解。为此,我们要先建立线性空间、特征向量的概念。如果你是一个新手,你大可以把他当做一个没有维数限制的欧氏空间。

下面,我们将亲手构造一个线性空间:

终于我们可以给一个平平无奇的定理

当然,我们还有一个平平无奇的定理

上面这两个定理的证明请参见任一泛函分析讲义。
接下来,我们需要知道左移算子L,它已经超越了“很好”,甚至可以用“无敌”来形容,它在V上的特征值和特征子空间长得十分规整,换句话说,你要问:什么数列是左移不变(等于没移)的?
答案只有一个:等比数列。

现在,你对Fibonacci数列是不是有更深刻的理解了呢~