本月,我们一起来挑战一道USAMO中较为困难的问题,并看看机构的老师给我们提供了怎么样的解题思路——
每月一题
2020 USAMO Problem 6

A 证明:首先要通过一些小的n,得到取等条件:
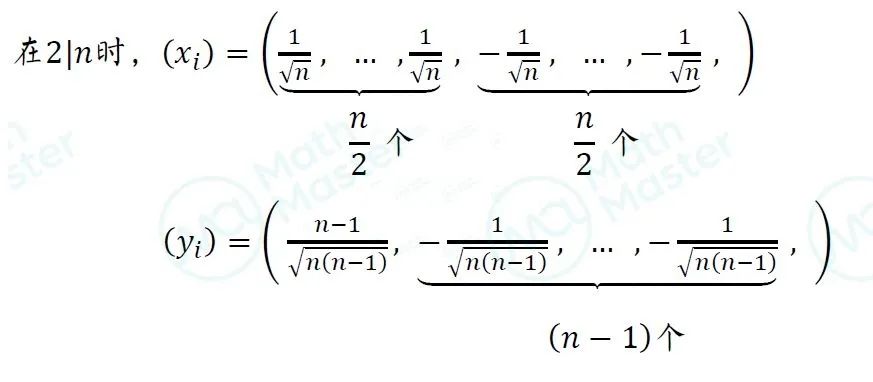
solution 1



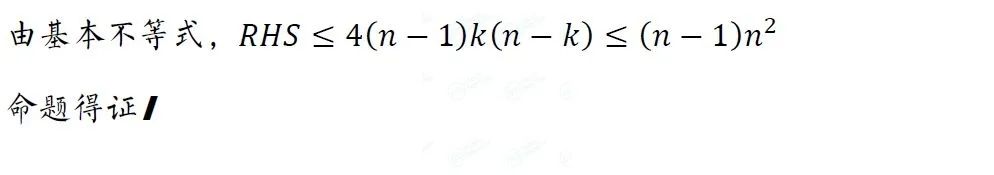
可以看到,本题的代数证明非常复杂,笔者参考了Anyndche的解答,并修改了其中一些明显的错误之处。虽然以上的证明已经可以作为USAMO的完整解答,但我们可以进一步观察题干,发现要证的结论与我们熟知的Chebyshev不等式类似,但离散情形的Chebyshev不等式仅能得到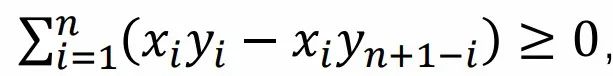 ,又结合
,又结合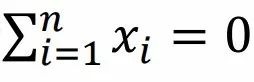 和
和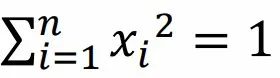 ,让我们可以联想到概率论中的Chebyshev不等式的思想,使用期望方法解决它。
,让我们可以联想到概率论中的Chebyshev不等式的思想,使用期望方法解决它。
solution 2


以上证明反映了本题深刻的数学背景,它包含了抽象代数中的置换概念,概率论中方差的性质,本题也启发大家在学习概率论时,一定要认真理解期望、随机变量等概念,熟悉它们的计算。












