由AMC10/12难题背景延伸的图论知识

 A

在2021年AMC12A卷23题（也是AMC10A卷的23题），出现了上图这样的问题。虽然在AMC中，沿方格行走的有关概率、计数的问题时常出现，但本题使用的新型规则“wrap around”也即在跳到边上时再跳一步，可以跳到对边的规则，着实让许多同学在考场上摸不着头脑，在AMC10/12的课程中同学们学习过的对称方法由此失效。

在本题中，由机构冯老师提供的方法是比较考验仔细程度的分步概率方法，也不易在考试时想到；事实上，这样的问题有强烈的图论背景，如果大家能够学会把图形的图论背景抽象出来，那许多困难的、类似的题目会简单许多。

下面先给几个定义：

Def1

一个图G,是一些顶点(vertex)和边（edge)构成的集合

如：

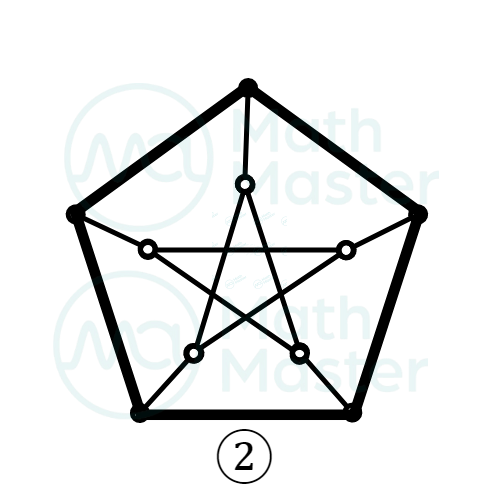
从以上的定义可见，两顶点之间边的样式并不重要，我们只关心他们之间是否连了边，以及连了几条边

Def2

两顶点V1与V2相邻，指它们之间存在边，记作V1~V2

顶点V的度（degree)是指与它相邻的顶点个数,记作d(v),如②中d(u)=3

Def3

若图G中有几个顶点，每个顶点的度都为K，则G为k-regular n-vertex graph

Def4

若图G中任两个顶点V1、V2之间连的边数不超过1（V1可以等于V2）称G为simple graph

Def5

一条路（path）是一组顶点（V1,V2……VK+1）使Vi~Vi+1,i=1,2,…..k,且i≠j时，Vi≠Vj，定义path的length为k,记为k-path.

定义path的length为k,记为k-path.

Def6

K_n称为n阶完全图，即n-vertex graph中，任两个顶点都有且仅有一条边

如：

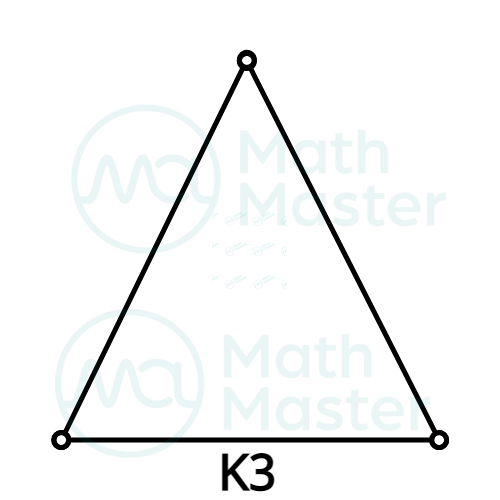
Note: K_n的每个顶点为n-1度

有了以上定义，我们来看一下今年这道AMC12A卷23题（也是AMC10A卷的23题），并尝试抽象出其图论性质，我们将3×3的方格中每一方格看作一个vertex，并且定义两个vertex x y相邻if and only if Frieda可以一步从X走到Y或从Y走到X这样，可见本题实际上是个9-vertex 4-regular graph

如图所示：C、A、G、I 为题所要求的终点，E为起点，现在使用分步求概率就避免了跳跃

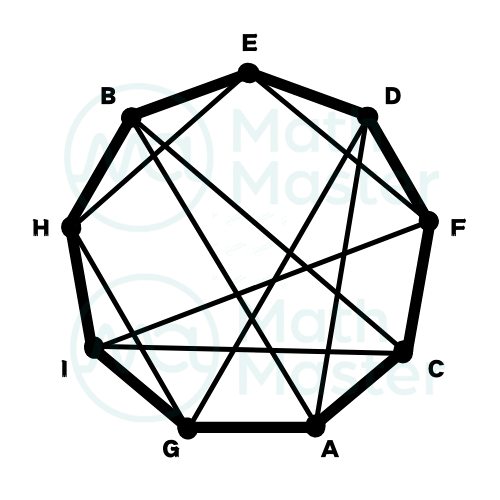
也许有同学会问，这样的图总存在吗？

比如k-regular n-vertex graph是否总是可以画在此，

有个定理可以回答：

结语：通过简单的定义，希望同学们学会抽象图论性质简化问题，明白Erdős-Gallai保证的存在。