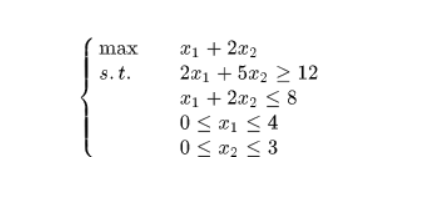
1、什么是线性规化?
线性规划(Linear programming,简称LP),是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。关键在于选定适当的决策变量。
2、线性规化简介
数学模型:
(1)列出约束条件及目标函数
(2)画出约束条件所表示的可行域
(3)在可行域内求目标函数的最优解及最优值
3、模型建立
从实际问题中建立数学模型一般有以下三个步骤;
1.根据影响所要达到目的的因素找到决策变量;
2.由决策变量和所在达到目的之间的函数关系确定目标函数;
3.由决策变量所受的限制条件确定决策变量所要满足的约束条件。
接下来让我们通过几个具体实例来体会“线性规划”在建模方面的实际应用
运输问题
例:
某商品有m个产地,n个销地,各产地的产量分别为a1,…,am,各销地的需求量分别为b1,…,bm。若该商品由i产地运到j销地的单位运价为c(ij),问应该如何调运才能使总运费最省?

01、产销平衡
存在产销平衡问题(当有也有生产与销售量不平衡的情况),实际上不平衡的运输问题可以转换成平衡型的问题。通过虚设一个产地或销售地并令运输成本为0。
02、解
当产量等于销售量的时候有可行解且必有最优解。并且若产量与销售量均为整数时,必存在决策变量均是整数的解。
03、表上作业法
其约束条件的系数矩阵相当特殊,可用比较简单的计算方法,习惯上称为表上作业法(由康托洛维奇和希奇柯克两人独立地提出,简称康—希表上作业法)。
指派问题
例:
拟分配n人去干n项工作,每人干且仅干一项工作,若分配第i人去干第j项工作,需花费C(ij)单位时间,问应如何分配工作才能使工人花费的总时间最少?


01、矩阵表示法
指派问题的可行解可以用一个矩阵表示,其每行每列均有且只有一个元素为1,其余元素均为 0;问题中的变量只能取 0 或1,从而是一个0-1 规划问题。一般的0-1 规划问题求解极为困难。但指派问题并不难解,其约束方程组的系数矩阵十分特殊(被称为全单位模矩阵,其各阶非零子式均为±1),其非负可行解的分量只能取 0或 1,故约束xijxij = 0或1可改写为xijxij≥ 0而不改变其解。此时,指派问题被转化为一个特殊的运输问题。
02、费药类
由于指派问题的特殊性,又存在着由匈牙利数学家 Konig 提出的更为简便的解法—匈牙利算法。算法主要依据:
如果系数矩阵 C=(cij)C=(cij)一行(或一列)中每一元素都加上或减去同一个数,得到一个新矩阵BB,则以C或B为系数矩阵的指派问题具有相同的最优指派。
对偶理论与灵敏度分析
对偶问题的基本性质:
01、对称性
对偶问题的对偶是原问题。
02、无界性
若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解。
03、对偶定理
若原问题有最优解,那么对偶问题也有最优解;且目标函数值相同。
03、互补松弛性
若xˆ,yˆx^,y^分别是原问题和对偶问题的最优解,则
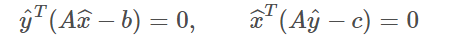
本期的建模算法之线性规划小知识到此告一段落啦。如果你对该算法有兴趣,可以自己动一动手去查找资料更深入了解一下。以下书籍供参考。

愿你在建模道路上越走越远!
最终满载而归!