TOPSIS算法是一种常用的综合评价方法,其能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距
Technique for Order Preference by Similarity to Ideal Solution可翻译为逼近理想解排序法,国内常简称为优劣解距离法。
一、算法理论部分
对于TOPSIS算法的理论介绍,小编将以曾经在大二时学习的笔记作为分享演示,当时学习的是清风数学建模,也算是作为一个怀念吧~



言归正传,基本过程为先将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,再对正向化的矩阵进行标准化处理以消除各指标量纲的影响,并找到有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。下面我们开始对TOPSIS的算法理论娓娓道来。
第一步:将原始矩阵正向化有常见的四种指标!
所谓的将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标。(转换的函数形式可以不唯一哦~ )
其中的四种指标如下图所示:
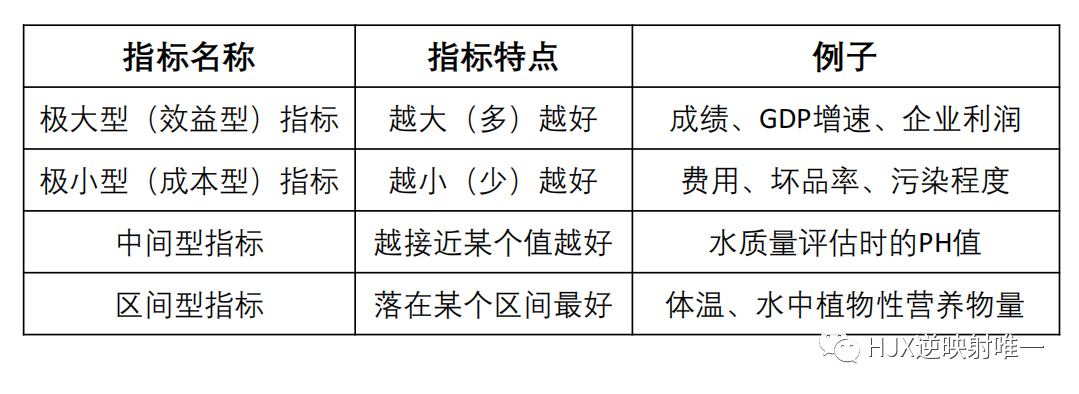
图1 正向化时的四种指标
(1)对于:极小型指标——>极大型指标

(2)对于:中间型指标——>极大型指标
中间型指标:指标值既不要太大也不要太小,取某特定值最好(如水质量评估 PH 值)。例子:

(3)对于:区间型指标——>极大型指标
区间型指标:指标值落在某个区间内最好,例如人的体温在36°~37°这个区间比较好。例子:

第二步:正向化矩阵标准化
(标准化的目的是消除不同指标量纲的影响)
注意:标准化的方法有很多种,主要目的就是去除量纲的影响,未来我们还可能见到更多种的标准化方法,例如:(x‐x的均值)/x的标准差;具体选用哪一种标准化的方法在多数情况下并没有很大的限制,这里我们采用的是比较多的一种标准化方法。

第三步:计算得分并归一化

二、TOPSIS算法模型的应用
案例:评价下表中20条河流的水质情况
(数据是随手编的,仅用于讲解相应的算法,可能有不合理之处,请见谅)
表1 20条河流的水质情况汇总
| 河流 | 含氧量(ppm) | PH值 | 细菌总数(个/mL) | 植物性营养物量(ppm) |
| A | 4.69 | 6.59 |
51 |
11.94 |
| B | 2.03 | 7.86 | 19 | 6.46 |
| C | 9.11 | 6.31 | 46 | 8.91 |
| D | 8.61 | 7.05 | 46 | 26.43 |
| E | 7.13 | 6.5 | 50 | 23.57 |
| F | 2.39 | 6.77 | 38 | 24.62 |
| G | 7.69 | 6.79 | 38 | 6.01 |
| H | 9.3 | 6.81 | 27 | 31.57 |
| I | 5.45 | 7.62 | 5 | 18.46 |
| J | 6.19 | 7.27 | 17 | 7.51 |
| K | 7.93 | 7.53 | 9 | 6.52 |
| L | 4.4 | 7.28 | 17 | 25.3 |
| M | 7.46 | 8.24 | 23 | 14.42 |
| N | 2.01 | 5.55 | 47 | 26.31 |
| O | 2.04 | 6.4 | 23 | 17.91 |
| P | 7.73 | 6.14 | 52 | 15.72 |
| Q | 6.35 | 7.58 | 25 | 29.46 |
| R | 8.29 | 8.41 | 39 | 12.02 |
| S | 3.54 | 7.27 | 54 | 3.16 |
| T | 7.44 | 6.26 | 8 | 28.41 |
对于上表的数据,我们可以确定出有20个评价对象(A--T),有4列评价指标,分别是:含氧量、PH值、细菌总数、植物性营养物量。
我们规定:含氧量越高越好;PH值越接近7越好;细菌总数越少越好;植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。
所以可以知道含氧量为极大型指标(不需要正向化处理),PH值为中间型指标(需要正向化处理),细菌总数为极小型指标(需要正向化处理),植物性营养物量为区间型指标(需要正向化处理)。
利用MATLAB进行算法编程与建模求解,并给出算法代码的详细注释与MATLAB求解的过程展示。
算法代码的详细注释
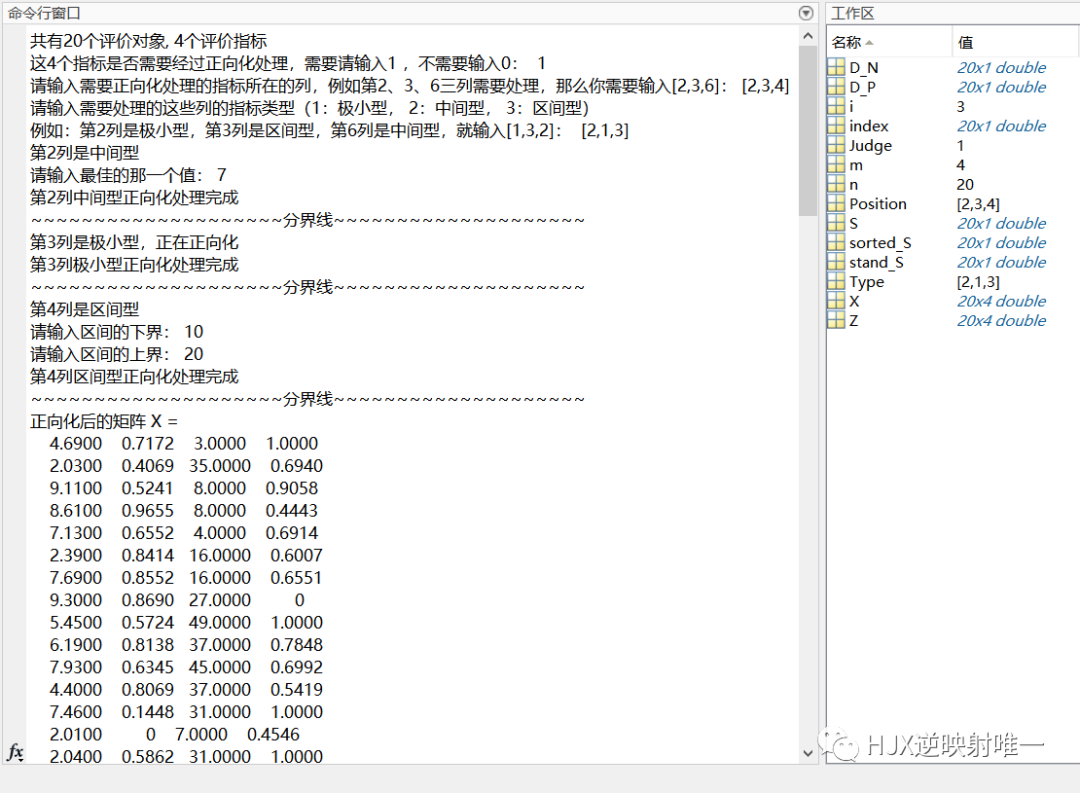
第一步:首先读取数据
第一步:把数据复制到工作区,并将这个矩阵命名为X % (1)在工作区右键,点击新建(Ctrl+N),输入变量名称为X % (2)在Excel中复制数据,再回到Excel中右键,点击粘贴Excel数据(Ctrl+Shift+V) % (3)关掉这个窗口,点击X变量,右键另存为,保存为mat文件(下次就不用复制粘贴了,只需使用load命令即可加载数据) % (4)注意,代码和数据要放在同一个目录下哦,且Matlab的当前文件夹也要是这个目录。 clear;clc load data_water_quality.mat %data_water_quality.mat为案例数据
第二步:判断是否需要正向化
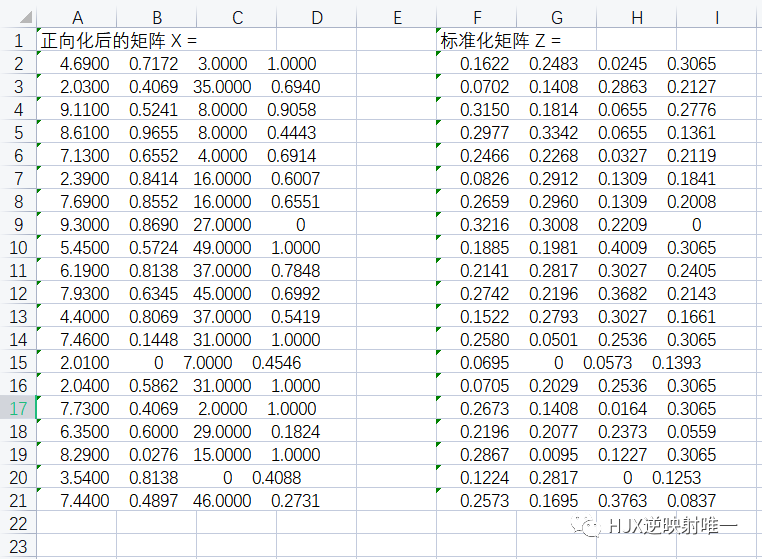
第二步:判断是否需要正向化 [n,m] = size(X); disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0:']); if Judge == 1 Position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]:'); %[2,3,4] disp('请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ') Type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]:'); %[2,1,3] % 注意,Position和Type是两个同维度的行向量 for i = 1 : size(Position,2) %这里需要对这些列分别处理,因此我们需要知道一共要处理的次数,即循环的次数 X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i)); % Positivization是我们自己定义的函数,其作用是进行正向化,其一共接收三个参数 % 第一个参数是要正向化处理的那一列向量 X(:,Position(i)) , X(:,n)表示取第n列的全部元素 % 第二个参数是对应的这一列的指标类型(1:极小型, 2:中间型, 3:区间型) % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列 % 该函数有一个返回值,它返回正向化之后的指标,我们可以将其直接赋值给我们原始要处理的那一列向量 end disp('正向化后的矩阵 X = ') disp(X) end
第三步:对正向化后的矩阵进行标准化
第三步:对正向化后的矩阵进行标准化 Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1); disp('标准化矩阵 Z = ') disp(Z)
第四步:计算与最大值的距离和最小值的距离,并算出得分
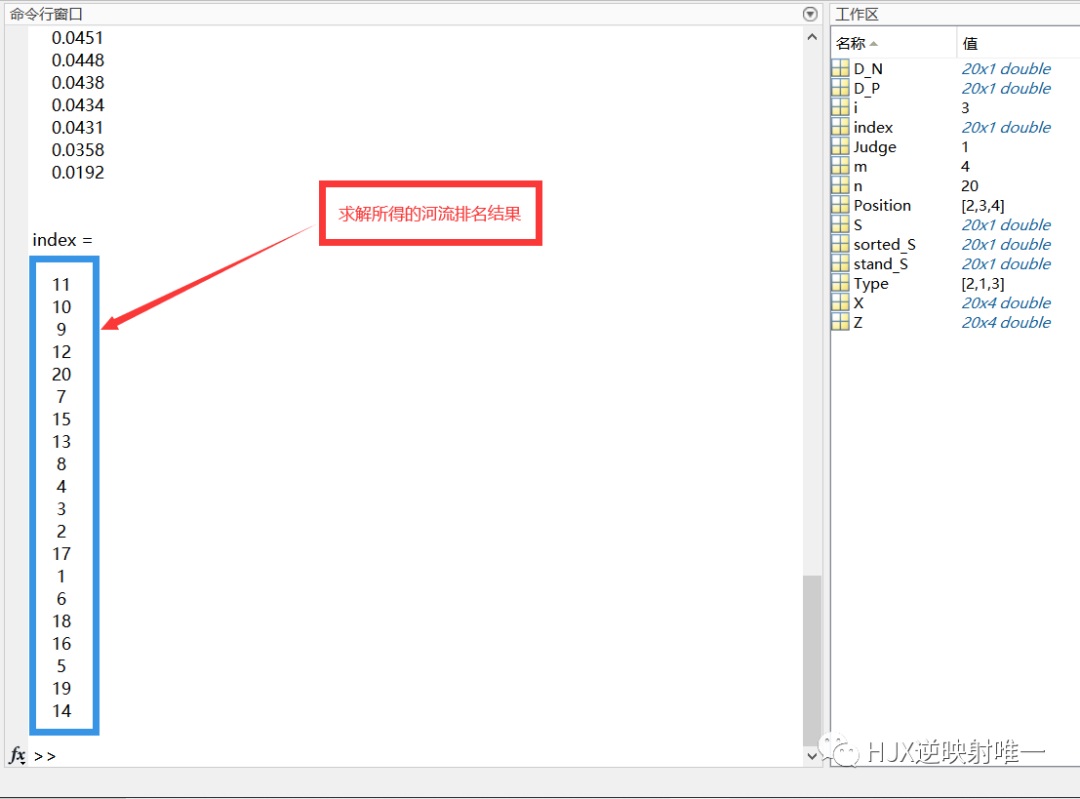
第四步:计算与最大值的距离和最小值的距离,并算出得分 D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5; % D+ 与最大值的距离向量 D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5; % D- 与最小值的距离向量 S = D_N ./ (D_P+D_N); % 未归一化的得分 disp('最后的得分为:') stand_S = S / sum(S) [sorted_S,index] = sort(stand_S ,'descend')
使用MATLAB编写的TOPSIS算法中定义的函数如下
Positivization函数定义的代码:
注意:自定义的函数要单独放在一个m文件中,不可以直接放在主函数里面(和其他大多数语言不同) function [posit_x] = Positivization(x,type,i) % 输入变量有三个: % x:需要正向化处理的指标对应的原始列向量 % type: 指标的类型(1:极小型, 2:中间型, 3:区间型) % i: 正在处理的是原始矩阵中的哪一列 % 输出变量posit_x表示:正向化后的列向量 if type == 1 %极小型 disp(['第' num2str(i) '列是极小型,正在正向化'] ) posit_x = Min2Max(x); %调用Min2Max函数来正向化 disp(['第' num2str(i) '列极小型正向化处理完成'] ) disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~') elseif type == 2 %中间型 disp(['第' num2str(i) '列是中间型'] ) best = input('请输入最佳的那一个值: '); posit_x = Mid2Max(x,best); disp(['第' num2str(i) '列中间型正向化处理完成'] ) disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~') elseif type == 3 %区间型 disp(['第' num2str(i) '列是区间型'] ) a = input('请输入区间的下界: '); b = input('请输入区间的上界: '); posit_x = Inter2Max(x,a,b); disp(['第' num2str(i) '列区间型正向化处理完成'] ) disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~') else disp('没有这种类型的指标,请检查Type向量中是否有除了1、2、3之外的其他值') end end
Mid2Max函数定义的代码:
注意:自定义的函数要单独放在一个m文件中,不可以直接放在主函数里面(和其他大多数语言不同) function [posit_x] = Mid2Max(x,best) M = max(abs(x-best)); posit_x = 1 - abs(x-best) / M; end
Min2Max函数定义的代码:
注意:自定义的函数要单独放在一个m文件中,不可以直接放在主函数里面(和其他大多数语言不同) function [posit_x] = Min2Max(x) posit_x = max(x) - x; %posit_x = 1 ./ x; %如果x全部都大于0,也可以这样正向化 end
Inter2Max函数定义的代码:
注意:自定义的函数要单独放在一个m文件中,不可以直接放在主函数里面(和其他大多数语言不同) function [posit_x] = Inter2Max(x,a,b) r_x = size(x,1); % row of x M = max([a-min(x),max(x)-b]); posit_x = zeros(r_x,1); %zeros函数用法: zeros(3) zeros(3,1) ones(3) % 初始化posit_x全为0 初始化的目的是节省处理时间 for i = 1: r_x if x(i) < a posit_x(i) = 1-(a-x(i))/M; elseif x(i) > b posit_x(i) = 1-(x(i)-b)/M; else posit_x(i) = 1; end end end
MATLAB求解的过程展示
将MATLAB所求得的结果整理至Excel表格中:
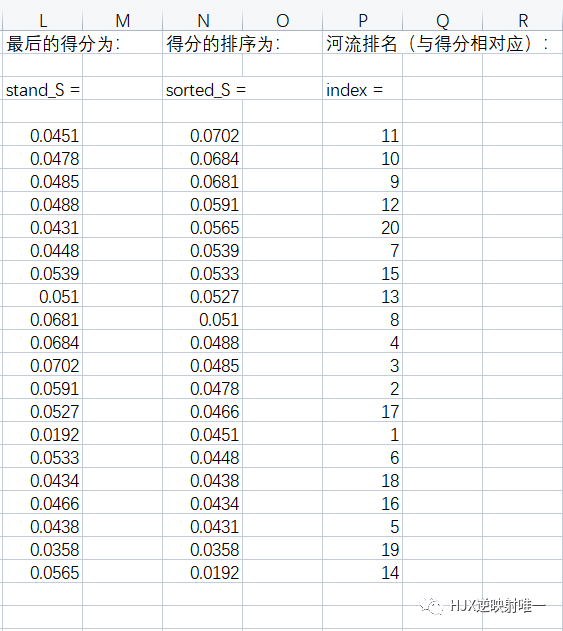
MATLAB的运算结果(河流排名)汇总
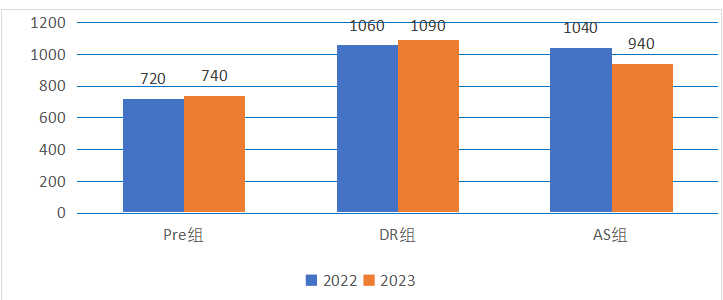
排名从高往低排序,可以看出得分最高的为K河流,得分最低的为N河流
表2 河流的水质得分排名情况
| 河流 | 含氧量(ppm) | PH值 | 细菌总数(个/mL) | 植物性营养物量(ppm) | 得分 |
| K | 7.93 | 7.53 | 9 | 6.52 | 0.070 |
| J | 6.19 | 7.27 | 17 | 7.51 | 0.068 |
| I | 5.45 | 7.62 | 5 | 18.46 | 0.068 |
| L | 4.4 | 7.28 | 17 | 25.3 | 0.059 |
| T | 7.44 | 6.26 | 8 | 28.41 | 0.056 |
| G | 7.69 | 6.79 | 38 | 6.01 | 0.054 |
| O | 2.04 | 6.4 | 23 | 17.91 | 0.053 |
| M | 7.46 | 8.24 | 23 | 14.42 | 0.053 |
| H | 9.3 | 6.81 | 27 | 31.57 | 0.051 |
| D | 8.61 | 7.05 | 46 | 26.43 | 0.049 |
| C | 9.11 | 6.31 | 46 | 8.91 | 0.048 |
| B | 2.03 | 7.86 | 19 | 6.46 | 0.048 |
| Q | 6.35 | 7.58 | 25 | 29.46 | 0.047 |
| A | 4.69 | 6.59 | 51 | 11.94 | 0.045 |
| F | 2.39 | 6.77 | 38 | 24.62 | 0.045 |
| R | 8.29 | 8.41 | 39 | 12.02 | 0.044 |
| P | 7.73 | 6.14 | 52 | 15.72 | 0.043 |
| E | 7.13 | 6.5 | 50 | 23.57 | 0.043 |
| S | 3.54 | 7.27 | 54 | 3.16 | 0.036 |
| N | 2.01 | 5.55 | 47 | 26.31 | 0.019 |
不同河流的得分可视化:
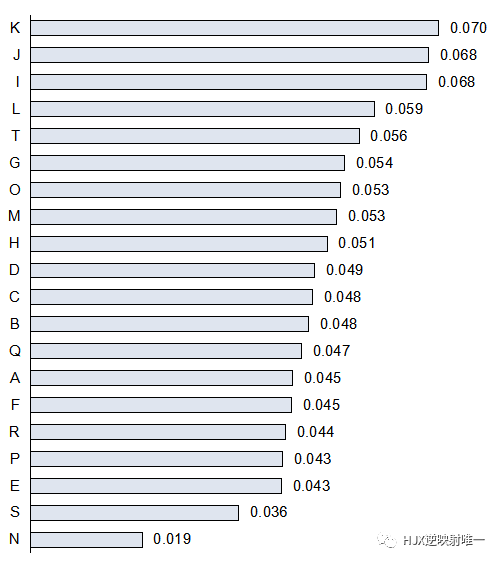
图2 河流的得分可视化
好啦!TOPSIS算法的案例演示就到此结束啦,感谢您的观看。
参考文献:
[1]菅毅,周金星,万龙,陈容,张梅,刘发万,丁玉雄.基于TOPSIS方法的喀斯特断陷盆地区番茄地下灌溉技术节水效益综合评价[J/OL].节水灌溉:1-13[2022-02-07].http://kns.cnki.net/kcms/detail/42.1420.TV.20220105.1358.002.htm.
[2]于小芹,马云瑞,余静.基于熵权TOPSIS模型的山东省海岸带生态修复政策效果评价研究[J].海洋环境科学,2022,41(01):74-79.DOI:10.13634/j.cnki.mes.2022.01.020.
[3]阳斌成,张家其,罗伟聪,喻兴洁,张兴苗.基于TOPSIS及耦合协调度的湖南省2009-2018年水资源承载力综合评价[J].水土保持通报,2021,41(05):357-364.DOI:10.13961/j.cnki.stbctb.2021.05.045.
[4]崔世华,于婧,陈艳红,韩晨晓.基于熵权TOPSIS的湖北省城市人居环境质量时空分异研究[J/OL].华中师范大学学报(自然科学版):1-11[2022-02-07].http://kns.cnki.net/kcms/detail/42.1178.n.20210830.1754.002.html.
[5]沈国辉,陈光,赵宇,李晓光,耿爱国,袁浩,刘方.基于双目标分层优化和TOPSIS排序的电动汽车有序充电策略[J].电力系统保护与控制,2021,49(11):115-123.DOI:10.19783/j.cnki.pspc.200955.