由于最近高强度更新的蒋氏数学内容过于硬核,今天给大家带来一点简单数学。
相信读者朋友们都有肉身不带雨伞过在大雨中奔跑的经历。我个人非常喜欢硕大雨点拍在脸上的感觉。每次在雨中行走时,我都会想,究竟是在雨中跑快点淋的雨少还是慢慢走淋的雨少呢?以前我猜测跑快点淋的雨多,因为明显雨点打在脸上更痛,不过也仅是猜测,没有严谨验证。接下来我将通过数学建模的方式来稍微研究一下。也就是研究移动速度和淋雨量的关系。
首先,假设的情景是:正在下雨,一个人在户外,想要从一个地方走到另一个地方,但他没有带雨伞或者雨衣。此时他想要找到一个最合适的速度移动过去而淋到最少的雨。跑还是不跑,这是个问题。
接下来是把这个现实情景简化成能够处理的模型。以下是模型的前提:
1. 这个人以匀速直线运动
2. 这个人是一个长方体
3. 降雨量稳定且没有风
以下是整个模型用到的所有乱七八糟的变量。大概看看就好,之后都会有详细解释。

要研究这个问题,首先要搞明白什么是雨。在这个模型中,雨应当被理解为一种类气体物质,或者叫“雨气”。它体积无限大,并以匀速垂直向下运动。它有两个重要的量:雨水密度ρ 和下落速度 VR。下落速度很好理解。雨水密度并不是指水的密度,而是在单位体积的“雨气”中水的质量。
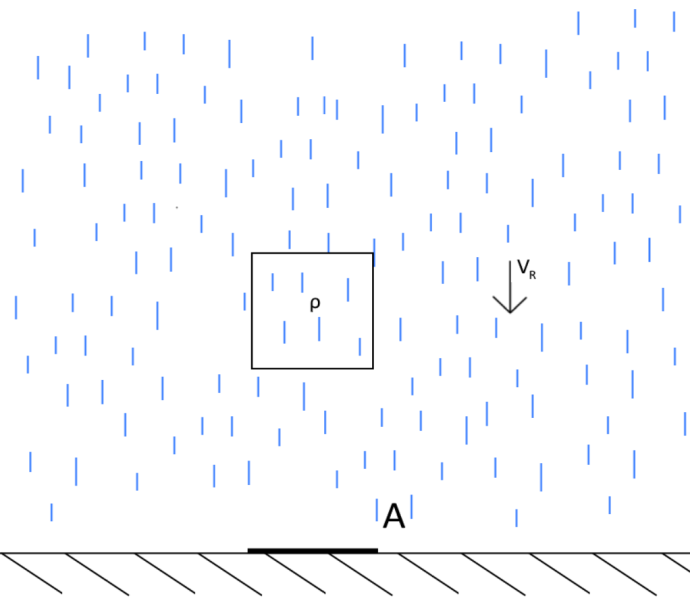
模型中的雨
上图展示了雨的两个性质。如果图中方块区域的雨气体积是1m3,那么这个区域中就包含了ρ千克的水。
再考虑地上面积为A的一块区域,这块区域单位时间内的淋雨量则为ρ * VR * A,单位为[kg/s]。经过t秒,这块区域就有M 千克的雨打在上面:
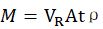
拓展到所有情况,也就是:
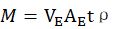
这个简单公式就是整个模型的核心。对于上图中的最简单情景,由于平面A是静止的,有效速度VE等于雨的下落速度VR。而平面和雨也没有夹角,有效面积AE等于平面面积A。
接下来将逐一解释VEAEtρ四个重要变量。
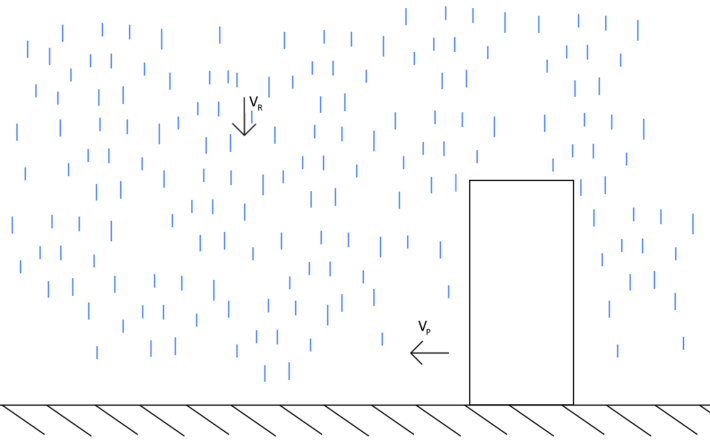
一个方块人在雨中移动
当一个(方块)人在雨中移动时,从图中可以看到两个速度,雨的下落速度VR和人的移动速度Vp. 为了方便分析,我们换个参考系,让人保持静止,把人的速度给加到雨的速度上。这样就会得到一个速度更快而且斜着的雨。

雨天坐高铁或飞机的时候可以看到斜着的雨
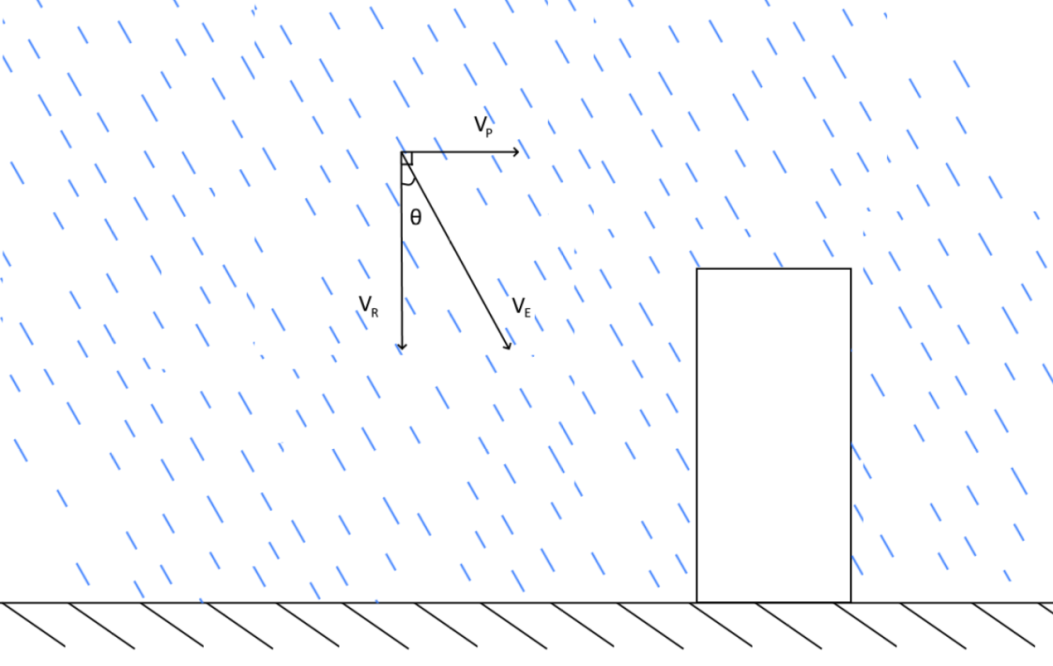
斜的雨
用一点三角函数和向量的知识,可以得到:
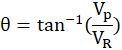
和
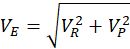
雨的角度和有效速度十分重要。角度决定了最终的有效面积,而有效速度直接影响淋雨量。很明显,当雨水密度一定时,雨的速度越快,那每秒打在身上的水就越多。
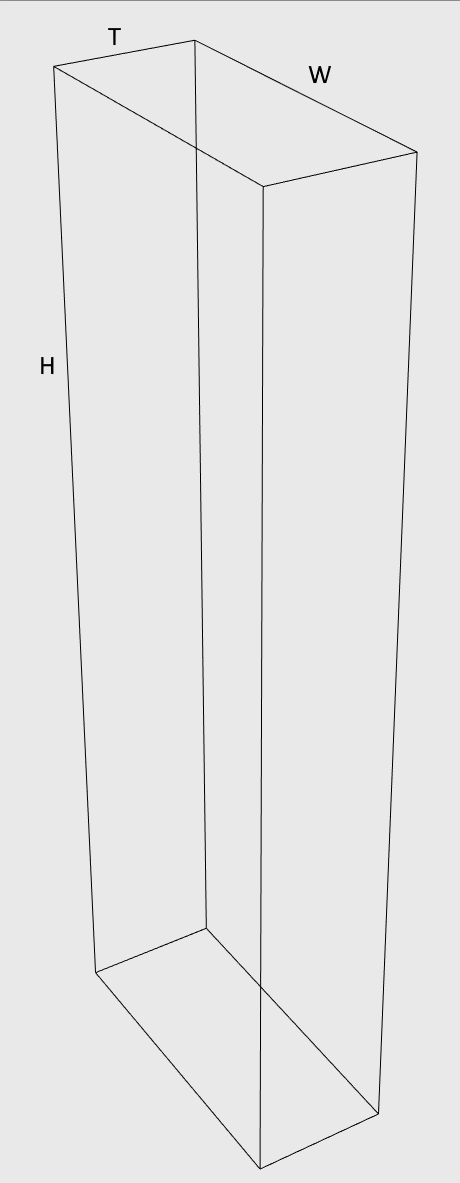
方块人
模型中的方块人高H米,宽W米,厚T米。由于我们假设无风,当他在雨中向前走的时候,只有正面和顶部会接触到雨。所以我们也只需要考虑正面和顶部的面积。
使用一些小学数学:
顶部面积 A1 = TW
正面面积 A2 = HW
由于雨可能是斜的,正面和顶部并不完全暴露在雨中,而是根据角度变化。此时就要考虑有效淋雨面积。
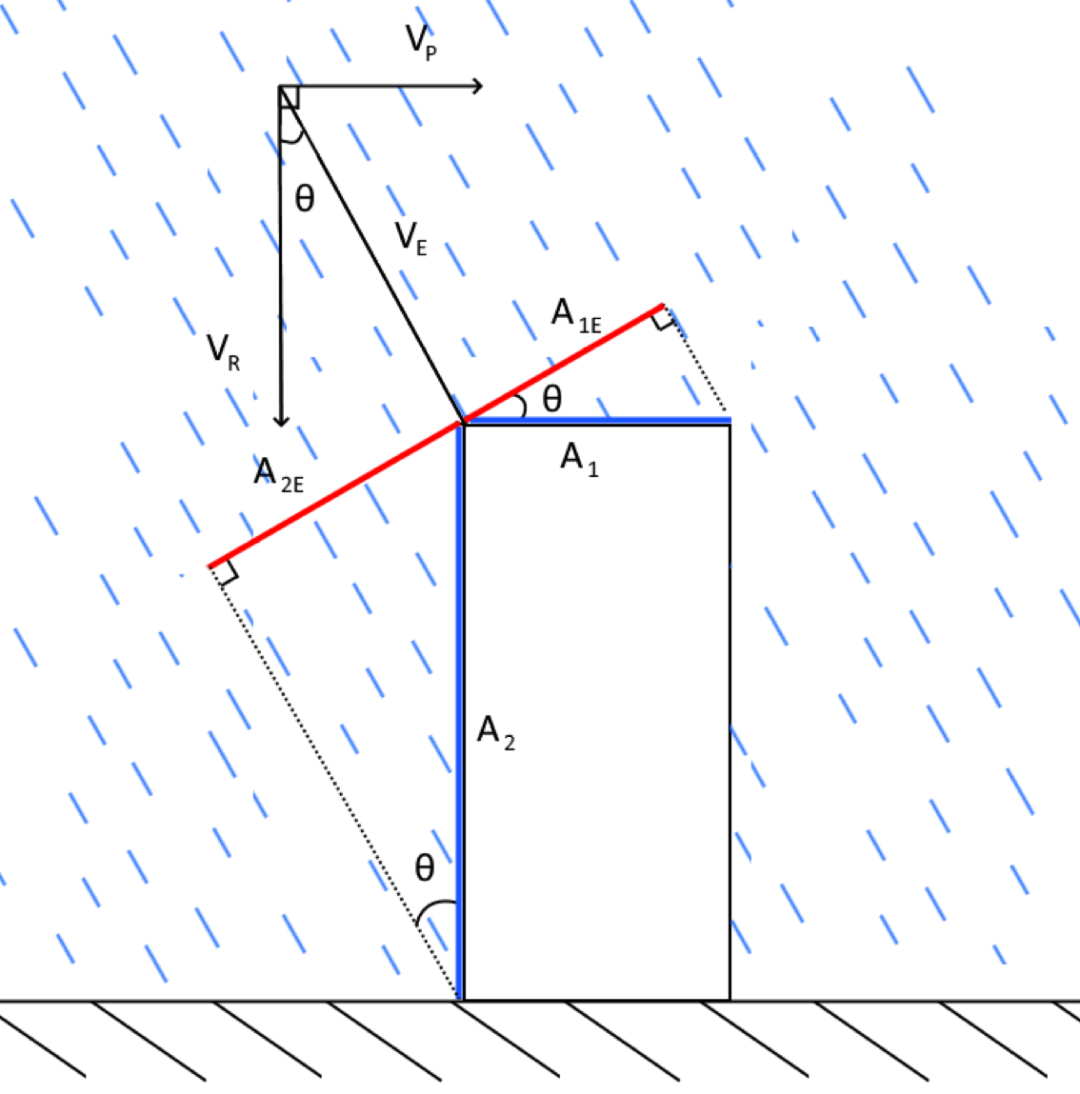
有效面积
上图中的蓝线代表方块人的真实面积,红线表示实际在淋雨的有效面积。再用一点初中三角函数来表示:
顶部有效面积 A1E = A1cos(θ)
正面有效面积 A2E = A2sin(θ)
总有效面积 AE = A1E + A2E
同时记得:
A1 = TW
A2 = HW
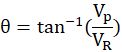
结合一下:
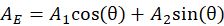
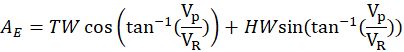
至此,相信大家已经轻松理解基础公式
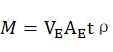
中的VE和AE,我们继续分析t和ρ。
这个人的目的地距离始发地的距离为d米,而他的速度为Vp。那么移动所耗的时间就是:
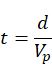
最后,我们要定义并解释最后一个变量ρ。
为了模型的准确性和适用性,我们最好能够使用真实的数据。首先我们来看一下现实中降雨量是如何表示的。日常生活中,读者朋友们肯定听说过“降雨量xx毫米”之类的播报。最常用的降雨量单位是[mm/m2/day],也就是“毫米每平方米每天”,简称“毫米”。
意思是一平方米的地面每天可以积累的雨水高度,等同于[L/m2/day],“升每平方米每天”。例如,如果我们说有一场降雨量为100mm的暴雨,那么意思就是这场雨中每天平方米土地都能积起100mm深的水(如果不排水),或者每平方米土地都被浇上了100L雨水。
仅使用降雨量的数据是不够的,我们还需要雨的速度。当雨滴在云层中形成后,它首先会因重力而向下加速,而后又因风阻和重力达到力平衡,最后雨滴将维持一个恒定的终端速度落地。根据一些论文,雨滴的终端速度与其体积有直接关系,而雨滴体积又与降雨量是直接相关的。降雨量越大,雨滴平均尺寸越大,终端速度也越高。
用降雨量,终端速度和液体密度来得到雨水密度:
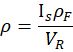
量纲分析验证一下准确性:
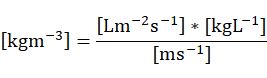
注意到此公式中用到的降雨量IS与常用降雨量IC单位不同,需要转换一下。例如,从[mm/m2/day]转换为:[Lm-2s-1]:
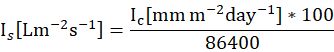
除了[mm m-2 day-1],还有一些其他的常用降雨量单位,如[mm m-2 hour-1],[mm m-2 month-1]和[mm m-2 year-1]。代入数据时稍稍转换一下即可。
至此,基本方程中的四个变量都解释完了,现在总结一下。
基本方程:
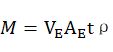
每个变量:
有效雨速度
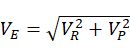
有效淋雨面积
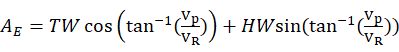
淋雨时间
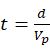
雨水密度
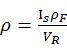
全部放在一起:
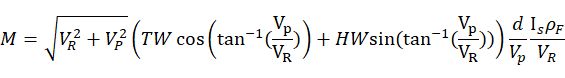
用这个公式就可以分析移动速度和淋雨量的关系了。M是应变量,VP是自变量,除此之外都是常量。接下来,我们将合适的常量代入进去来看看结果如何。
假设这个人高1.8米,宽1.5米,厚0.3米。他要走总共1000米直线。正在下雨。随便选了一个中雨的降雨量25 mm m-2 day-1,也就是0.00029 Lm-2s-1。
我们查一下这个降雨量下的雨滴终端速度。
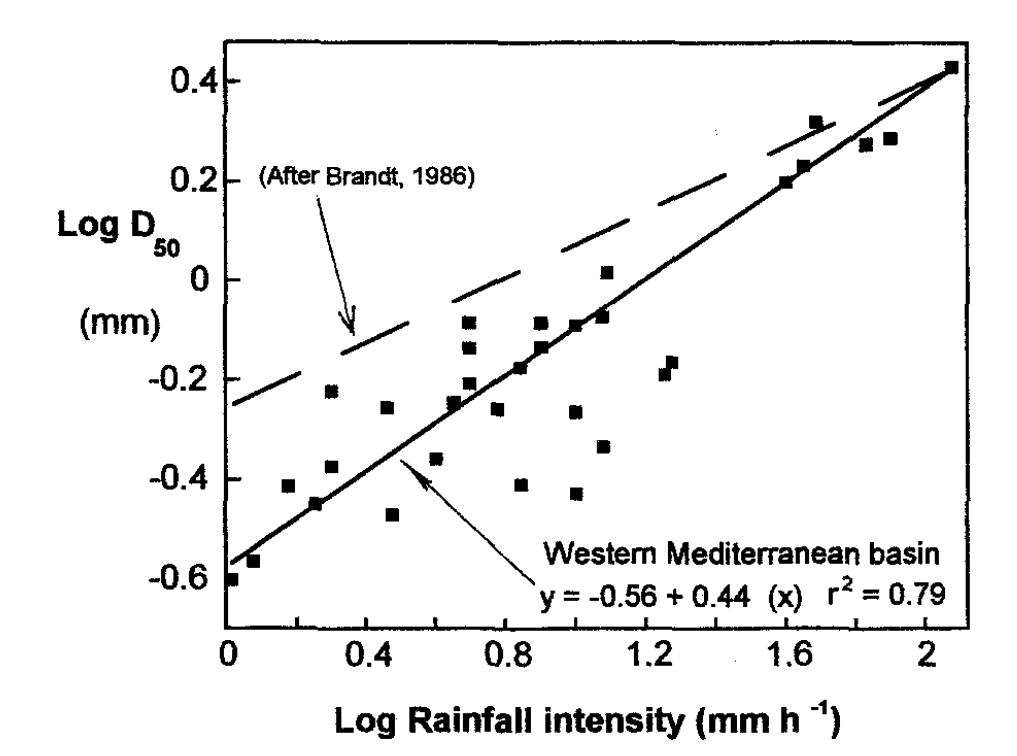
降雨量和雨滴直径的关系
(Cerdá, A. “Rainfall Drop Size Distribution in the Western Mediterranean Basin, València, Spain.” CATENA, vol. 30, no. 2-3, 1997, pp. 169–182., doi:10.1016/s0341-8162(97)00019-2.)
通过这篇论文收集分析的信息,我们可以找到降雨量和雨滴直径的关系。将25 mm m-2 day-1转换为上图中使用的单位,为1.04 mm m-2 hour-1。根据作者给出的趋势线:
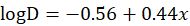
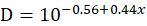
把1.04 mm m-2 hour-1代入,得到:
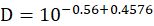
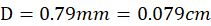
也就是说在这个降雨量下水滴的平均直径大约是0.079cm。
然后,我们再找到一篇研究雨滴尺寸和终端速度的论文。
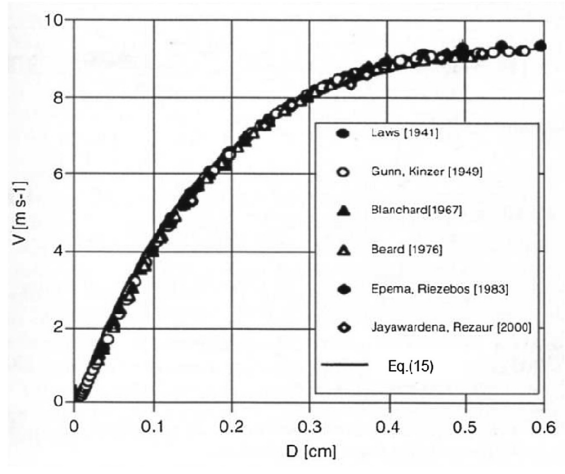
雨滴直径与终端速度的关系
(Serio, Maria A., et al. “Raindrop Size Distribution and Terminal Velocity for Rainfall Erosivity Studies. A Review.” Journal of Hydrology, vol. 576, 2019, pp. 210–228., doi:10.1016/j.jhydrol.2019.06.040.)
虽然作者给出了趋势线的公式,但我们可以方便点直接用大眼睛看图。当水滴直径为0.079cm时终端速度大概是2.7 ms-1.
把常量列一下:
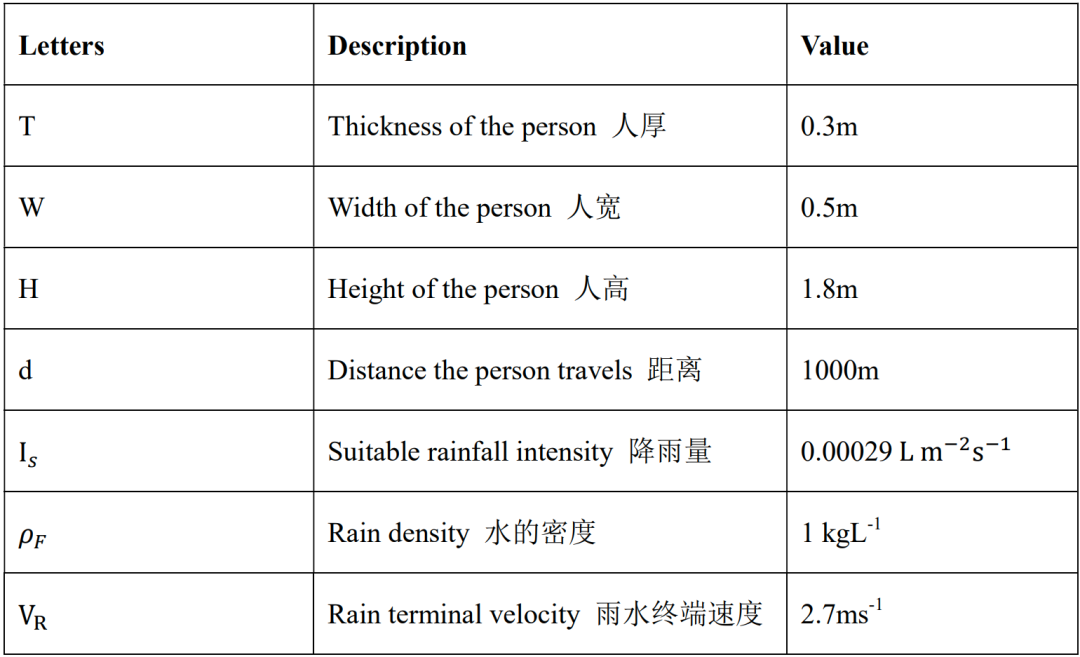
把这些量代入方程:
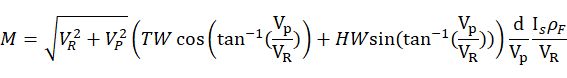
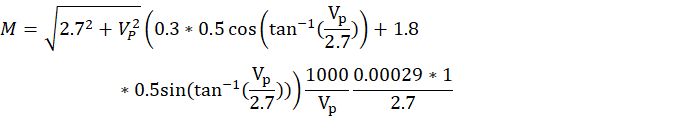
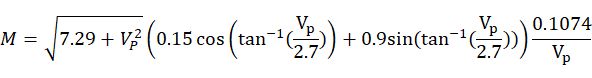
画个图
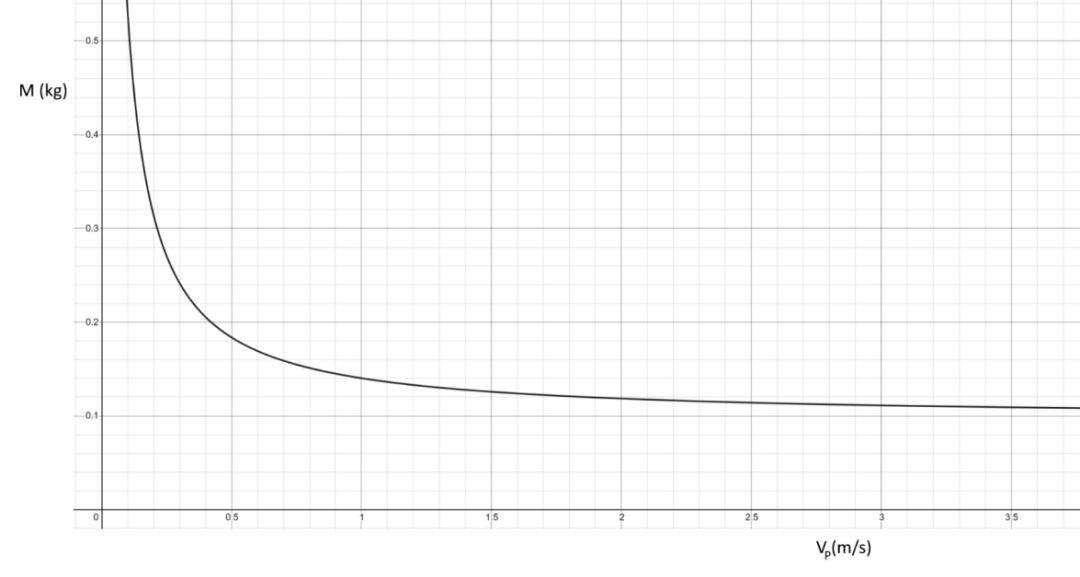
x轴是人的速度,y轴是总淋雨质量
从图中可以看出,人跑得越快淋雨就越少。但仅在低速有明显减少,高速情况下没啥区别。
事实上,就算人跑得无限快,也至少会淋到一定量的雨水。当Vp趋近于无限时:
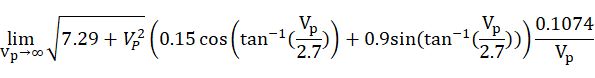
每项分开看,首先发现:
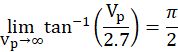
于是,含有三角函数的那一项变成常数:
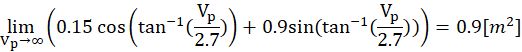
0.9放进去一起再看剩下的:
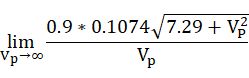
由于:
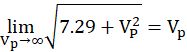
所以:
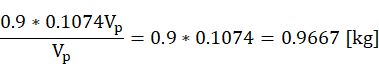
无论跑的多快,至少也要淋0.9667kg的雨。
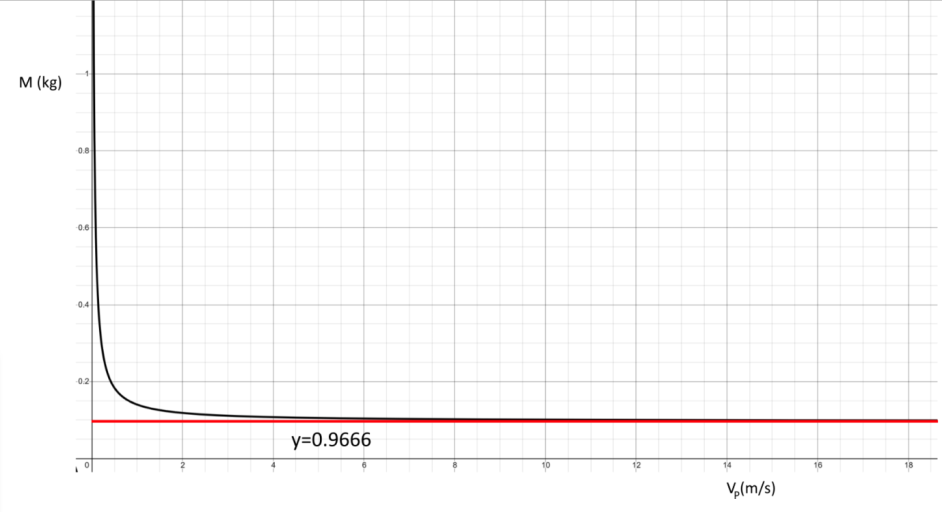
函数的渐近线
物理上验证:
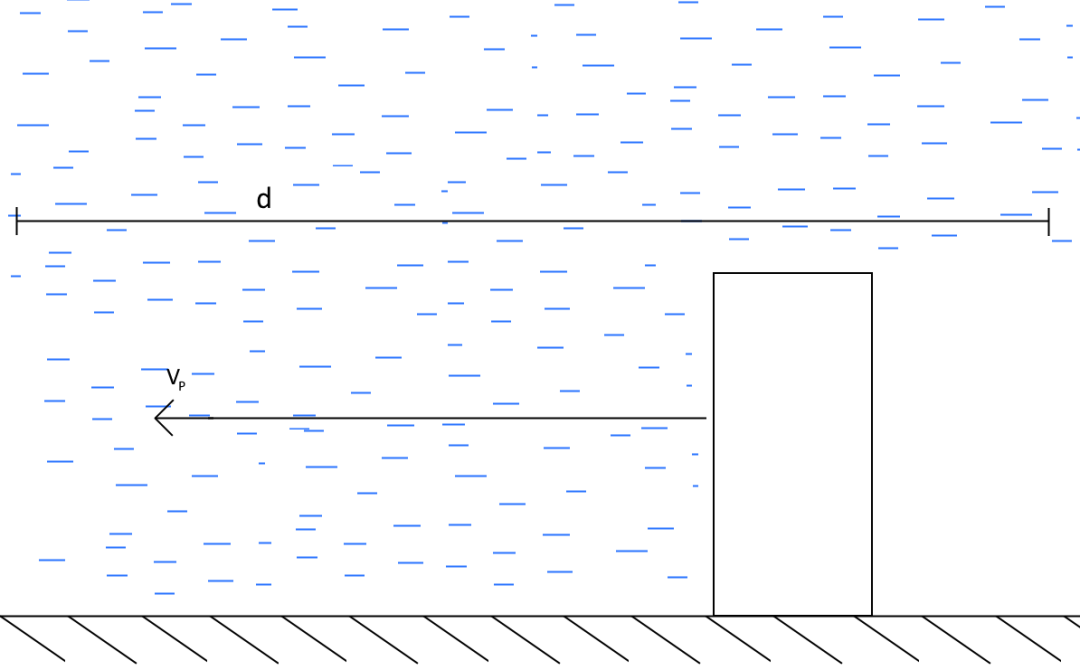
极高速下的情况
根据上图,当人的速度极高时,雨滴可以视为静止。这个人就会“横扫”过路径上的所有水滴。因此,总质量为:
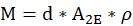
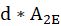
给出总扫过的雨气体积,ρ为雨气密度。
代入验证:
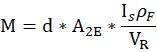
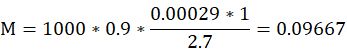
结果与之前一致。
结论:跑的快确实能减少淋到的雨,但是人是有极限的,跑的再快还是要淋雨。建议大家在不累死自己的前提下跑快点或者带把雨伞。












